Fit detection functions and calculate abundance from line or point transect data

This function fits detection functions to line or point transect data and then (provided that survey information is supplied) calculates abundance and density estimates. The examples below illustrate some basic types of analysis using ds().

Usage

ds(
  data,
  truncation = ifelse(is.null(cutpoints), ifelse(is.null(data$distend),
    max(data$distance), max(data$distend)), max(cutpoints)),
  transect = "line",
  formula = ~1,
  key = c("hn", "hr", "unif"),
  adjustment = c("cos", "herm", "poly"),
  nadj = NULL,
  order = NULL,
  scale = c("width", "scale"),
  cutpoints = NULL,
  dht_group = FALSE,
  monotonicity = ifelse(formula == ~1, "strict", "none"),
  region_table = NULL,
  sample_table = NULL,
  obs_table = NULL,
  convert_units = 1,
  er_var = ifelse(transect == "line", "R2", "P2"),
  method = "nlminb",
  mono_method = "slsqp",
  quiet = FALSE,
  debug_level = 0,
  initial_values = NULL,
  max_adjustments = 5,
  er_method = 2,
  dht_se = TRUE,
  optimizer = "both",
  winebin = NULL,
  dht.group,
  region.table,
  sample.table,
  obs.table,
  convert.units,
  er.var,
  debug.level,
  initial.values,
  max.adjustments
)

Arguments

data

a data.frame containing at least a column called distance or a numeric vector containing the distances. NOTE! If there is a column called size in the data then it will be interpreted as group/cluster size, see the section "Clusters/groups", below. One can supply data as a "flat file" and not supply region_table, sample_table and obs_table, see "Data format", below and flatfile.

truncation

either truncation distance (numeric, e.g. 5) or percentage (as a string, e.g. "15%"). Can be supplied as a list with elements left and right if left truncation is required (e.g. list(left=1,right=20) or list(left="1%",right="15%") or even list(left="1",right="15%")). By default for exact distances the maximum observed distance is used as the right truncation. When the data is binned, the right truncation is the largest bin end point. Default left truncation is set to zero.

transect

indicates transect type "line" (default) or "point".

formula

formula for the scale parameter. For a CDS analysis leave this as its default ~1.

key

key function to use; "hn" gives half-normal (default), "hr" gives hazard-rate and "unif" gives uniform. Note that if uniform key is used, covariates cannot be included in the model.

adjustment

adjustment terms to use; "cos" gives cosine (default), "herm" gives Hermite polynomial and "poly" gives simple polynomial. A value of NULL indicates that no adjustments are to be fitted.

nadj

the number of adjustment terms to fit. In the absence of covariates in the formula, the default value (NULL) will select via AIC (using a sequential forward selection algorithm) up to max.adjustment adjustments (unless order is specified). When covariates are present in the model formula, the default value of NULL results in no adjustment terms being fitted in the model. A non-negative integer value will cause the specified number of adjustments to be fitted. Supplying an integer value will allow the use of adjustment terms in addition to specifying covariates in the model. The order of adjustment terms used will depend on the keyand adjustment. For key="unif", adjustments of order 1, 2, 3, ... are fitted when adjustment = "cos" and order 2, 4, 6, ... otherwise. For key="hn" or "hr" adjustments of order 2, 3, 4, ... are fitted when adjustment = "cos" and order 4, 6, 8, ... otherwise. See Buckland et al. (2001, p. 47) for details.

order

order of adjustment terms to fit. The default value (NULL) results in ds choosing the orders to use - see nadj. Otherwise a scalar positive integer value can be used to fit a single adjustment term of the specified order, and a vector of positive integers to fit multiple adjustment terms of the specified orders. For simple and Hermite polynomial adjustments, only even orders are allowed. The number of adjustment terms specified here must match nadj (or nadj can be the default NULL value).

scale

the scale by which the distances in the adjustment terms are divided. Defaults to "width", scaling by the truncation distance. If the key is uniform only "width" will be used. The other option is "scale": the scale parameter of the detection

cutpoints

if the data are binned, this vector gives the cutpoints of the bins. Supplying a distance column in your data and specifying cutpoints is the recommended approach for all standard binned analyses. Ensure that the first element is 0 (or the left truncation distance) and the last is the distance to the end of the furthest bin. (Default NULL, no binning.) If you have provided distbegin and distend columns in your data (note this should only be used when your cutpoints are not constant across all your data, e.g. planes flying at differing altitudes) then do not specify the cutpoints argument as this will cause the distbegin and distend columns in your data to be overwritten.

dht_group

should density abundance estimates consider all groups to be size 1 (abundance of groups) dht_group=TRUE or should the abundance of individuals (group size is taken into account), dht_group=FALSE. Default is FALSE (abundance of individuals is calculated).

monotonicity

should the detection function be constrained for monotonicity weakly ("weak"), strictly ("strict") or not at all ("none" or FALSE). See Monotonicity, below. (Default "strict"). By default it is on for models without covariates in the detection function, off when covariates are present.

region_table

data_frame with two columns:

• Region.Label label for the region

• Area area of the region

• region_table has one row for each stratum. If there is no stratification then region_table has one entry with Area corresponding to the total survey area. If Area is omitted density estimates only are produced.

sample_table

data.frame mapping the regions to the samples (i.e. transects). There are three columns:

• Sample.Label label for the sample

• Region.Label label for the region that the sample belongs to.

• Effort the effort expended in that sample (e.g. transect length).

obs_table

data.frame mapping the individual observations (objects) to regions and samples. There should be three columns:

• object unique numeric identifier for the observation

• Region.Label label for the region that the sample belongs to

• Sample.Label label for the sample

convert_units

conversion between units for abundance estimation, see "Units", below. (Defaults to 1, implying all of the units are "correct" already.)

er_var

encounter rate variance estimator to use when abundance estimates are required. Defaults to "R2" for line transects and "P2" for point transects (>= 1.0.9, earlier versions <= 1.0.8 used the "P3" estimator by default for points). See dht2 for more information and if more complex options are required.

method

optimization method to use (any method usable by optim or optimx). Defaults to "nlminb".

mono_method

optimization method to use when monotonicity is enforced. Can be either slsqp or solnp. Defaults to slsqp.

quiet

suppress non-essential messages (useful for bootstraps etc). Default value FALSE.

debug_level

print debugging output. 0=none, 1-3 increasing levels of debugging output.

initial_values

a list of named starting values, see mrds_opt. Only allowed when AIC term selection is not used.

max_adjustments

maximum number of adjustments to try (default 5) only used when order=NULL.

er_method

encounter rate variance calculation: default = 2 gives the method of Innes et al, using expected counts in the encounter rate. Setting to 1 gives observed counts (which matches Distance for Windows) and 0 uses binomial variance (only useful in the rare situation where study area = surveyed area). See dht.se for more details.

dht_se

should uncertainty be calculated when using dht? Safe to leave as TRUE, used in bootdht.

optimizer

By default this is set to 'both'. In this case the R optimizer will be used and if present the MCDS optimizer will also be used. The result with the best likelihood value will be selected. To run only a specified optimizer set this value to either 'R' or 'MCDS'. See mcds_dot_exe for setup instructions.

winebin

If you are trying to use our MCDS.exe optimizer on a non-windows system then you may need to specify the winebin. Please see mcds_dot_exe for more details.

dht.group

deprecated, see same argument with underscore, above.

region.table

deprecated, see same argument with underscore, above.

sample.table

deprecated, see same argument with underscore, above.

obs.table

deprecated, see same argument with underscore, above.

convert.units

deprecated, see same argument with underscore, above.

er.var

deprecated, see same argument with underscore, above.

debug.level

deprecated, see same argument with underscore, above.

initial.values

deprecated, see same argument with underscore, above.

max.adjustments

deprecated, see same argument with underscore, above.

Value

a list with elements:

• ddf a detection function model object.

• dht abundance/density information (if survey region data was supplied, else NULL)

Details

If abundance estimates are required then the data.frames region_table and sample_table must be supplied. If data does not contain the columns Region.Label and Sample.Label then the data.frame obs_table must also be supplied. Note that stratification only applies to abundance estimates and not at the detection function level. Density and abundance estimates, and corresponding estimates of variance and confidence intervals, are calculated using the methods described in Buckland et al. (2001) sections 3.6.1 and 3.7.1 (further details can be found in the documentation for dht).

For more advanced abundance/density estimation please see the dht and dht2 functions.

Examples of distance sampling analyses are available at http://examples.distancesampling.org/.

Hints and tips on fitting (particularly optimisation issues) are on the mrds_opt manual page.

Clusters/groups

Note that if the data contains a column named size, cluster size will be estimated and density/abundance will be based on a clustered analysis of the data. Setting this column to be NULL will perform a non-clustered analysis (for example if "size" means something else in your dataset).

Truncation

The right truncation point is by default set to be largest observed distance or bin end point. This is a default will not be appropriate for all data and can often be the cause of model convergence failures. It is recommended that one plots a histogram of the observed distances prior to model fitting so as to get a feel for an appropriate truncation distance. (Similar arguments go for left truncation, if appropriate). Buckland et al (2001) provide guidelines on truncation.

When specified as a percentage, the largest right and smallest left percent distances are discarded. Percentages cannot be supplied when using binned data.

For left truncation, there are two options: (1) fit a detection function to the truncated data as is (this is what happens when you set left). This does not assume that g(x)=1 at the truncation point. (2) manually remove data with distances less than the left truncation distance – effectively move the centre line out to be the truncation distance (this needs to be done before calling ds). This then assumes that detection is certain at the left truncation distance. The former strategy has a weaker assumption, but will give higher variance as the detection function close to the line has no data to tell it where to fit – it will be relying on the data from after the left truncation point and the assumed shape of the detection function. The latter is most appropriate in the case of aerial surveys, where some area under the plane is not visible to the observers, but their probability of detection is certain at the smallest distance.

Binning

Note that binning is performed such that bin 1 is all distances greater or equal to cutpoint 1 (>=0 or left truncation distance) and less than cutpoint 2. Bin 2 is then distances greater or equal to cutpoint 2 and less than cutpoint 3 and so on.

Monotonicity

When adjustment terms are used, it is possible for the detection function to not always decrease with increasing distance. This is unrealistic and can lead to bias. To avoid this, the detection function can be constrained for monotonicity (and is by default for detection functions without covariates).

Monotonicity constraints are supported in a similar way to that described in Buckland et al (2001). 20 equally spaced points over the range of the detection function (left to right truncation) are evaluated at each round of the optimisation and the function is constrained to be either always less than it's value at zero ("weak") or such that each value is less than or equal to the previous point (monotonically decreasing; "strict"). See also check.mono.

Even with no monotonicity constraints, checks are still made that the detection function is monotonic, see check.mono.

Units

In extrapolating to the entire survey region it is important that the unit measurements be consistent or converted for consistency. A conversion factor can be specified with the convert_units argument. The values of Area in region_table, must be made consistent with the units for Effort in sample_table and the units of distance in the data.frame that was analyzed. It is easiest if the units of Area are the square of the units of Effort and then it is only necessary to convert the units of distance to the units of Effort. For example, if Effort was entered in kilometres and Area in square kilometres and distance in metres then using convert_units=0.001 would convert metres to kilometres, density would be expressed in square kilometres which would then be consistent with units for Area. However, they can all be in different units as long as the appropriate composite value for convert_units is chosen. Abundance for a survey region can be expressed as: A*N/a where A is Area for the survey region, N is the abundance in the covered (sampled) region, and a is the area of the sampled region and is in units of Effort * distance. The sampled region a is multiplied by convert_units, so it should be chosen such that the result is in the same units as Area. For example, if Effort was entered in kilometres, Area in hectares (100m x 100m) and distance in metres, then using convert_units=10 will convert a to units of hectares (100 to convert metres to 100 metres for distance and .1 to convert km to 100m units).

Data format

One can supply data only to simply fit a detection function. However, if abundance/density estimates are necessary further information is required. Either the region_table, sample_table and obs_table data.frames can be supplied or all data can be supplied as a "flat file" in the data argument. In this format each row in data has additional information that would ordinarily be in the other tables. This usually means that there are additional columns named: Sample.Label, Region.Label, Effort and Area for each observation. See flatfile for an example.

Density estimation

If column Area is omitted, a density estimate is generated but note that the degrees of freedom/standard errors/confidence intervals will not match density estimates made with the Area column present.

References

Buckland, S.T., Anderson, D.R., Burnham, K.P., Laake, J.L., Borchers, D.L., and Thomas, L. (2001). Distance Sampling. Oxford University Press. Oxford, UK.

Buckland, S.T., Anderson, D.R., Burnham, K.P., Laake, J.L., Borchers, D.L., and Thomas, L. (2004). Advanced Distance Sampling. Oxford University Press. Oxford, UK.

See also

flatfile, AIC.ds, ds.gof, p_dist_table, plot.ds, add_df_covar_line

Author

David L. Miller

Examples

# An example from mrds, the golf tee data.
library(Distance)
data(book.tee.data)
tee.data <- subset(book.tee.data$book.tee.dataframe, observer==1)
ds.model <- ds(tee.data, 4)
#> Starting AIC adjustment term selection.
#> Fitting half-normal key function
#> AIC= 311.138
#> Fitting half-normal key function with cosine(2) adjustments
#> AIC= 313.124
#> 
#> Half-normal key function selected.
#> No survey area information supplied, only estimating detection function.
summary(ds.model)
#> 
#> Summary for distance analysis 
#> Number of observations :  124 
#> Distance range         :  0  -  4 
#> 
#> Model       : Half-normal key function 
#> AIC         :  311.1385 
#> Optimisation:  mrds (nlminb) 
#> 
#> Detection function parameters
#> Scale coefficient(s):  
#>              estimate         se
#> (Intercept) 0.6632435 0.09981249
#> 
#>                        Estimate          SE         CV
#> Average p             0.5842744  0.04637627 0.07937412
#> N in covered region 212.2290462 20.85130344 0.09824906
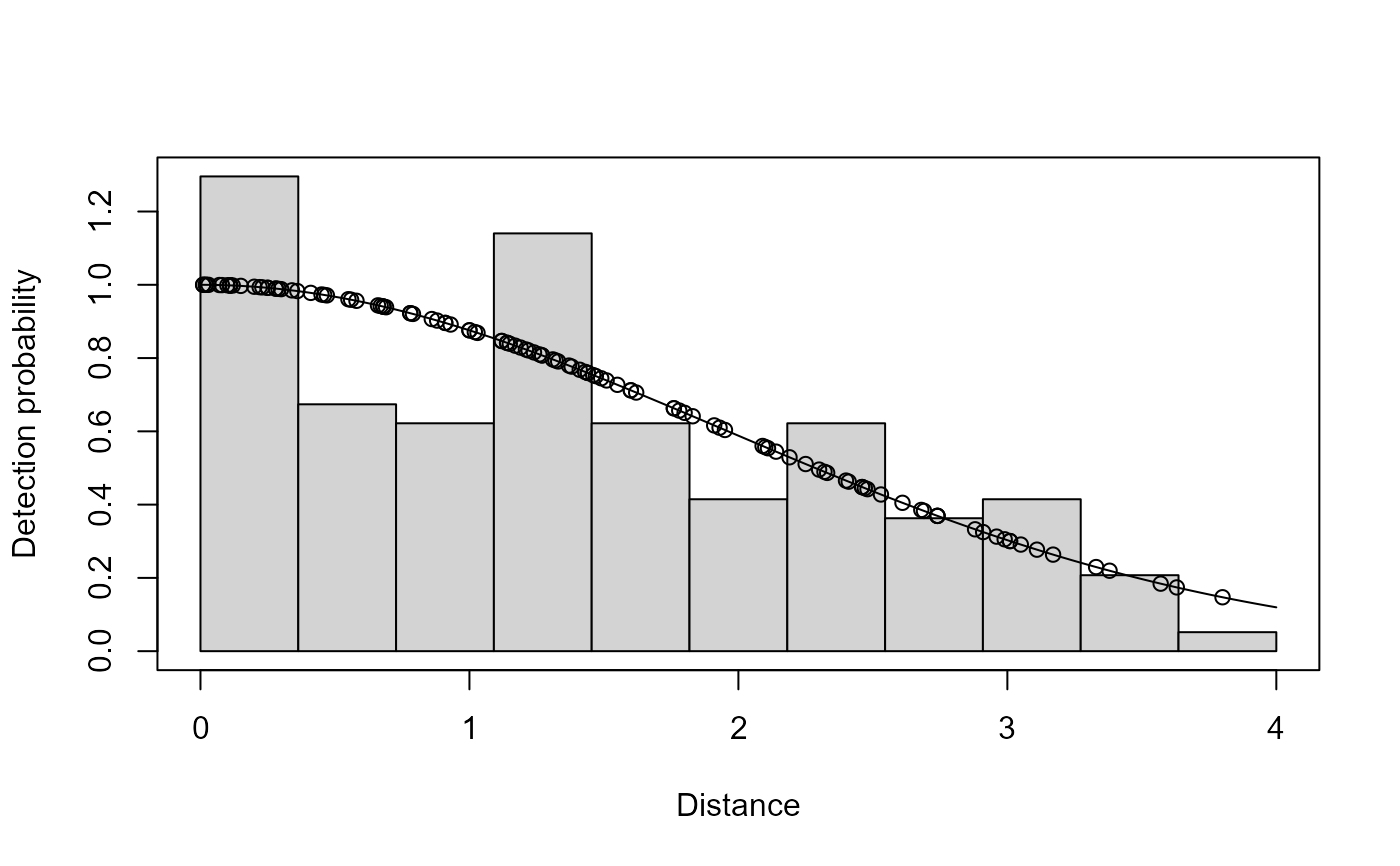
plot(ds.model)


# same model, but calculating abundance
# need to supply the region, sample and observation tables
region <- book.tee.data$book.tee.region
samples <- book.tee.data$book.tee.samples
obs <- book.tee.data$book.tee.obs

ds.dht.model <- ds(tee.data, 4, region_table=region,
                   sample_table=samples, obs_table=obs)
#> Starting AIC adjustment term selection.
#> Fitting half-normal key function
#> AIC= 311.138
#> Fitting half-normal key function with cosine(2) adjustments
#> AIC= 313.124
#> 
#> Half-normal key function selected.
summary(ds.dht.model)
#> 
#> Summary for distance analysis 
#> Number of observations :  124 
#> Distance range         :  0  -  4 
#> 
#> Model       : Half-normal key function 
#> AIC         :  311.1385 
#> Optimisation:  mrds (nlminb) 
#> 
#> Detection function parameters
#> Scale coefficient(s):  
#>              estimate         se
#> (Intercept) 0.6632435 0.09981249
#> 
#>                        Estimate          SE         CV
#> Average p             0.5842744  0.04637627 0.07937412
#> N in covered region 212.2290462 20.85130344 0.09824906
#> 
#> Summary for clusters
#> 
#> Summary statistics:
#>   Region Area CoveredArea Effort   n  k        ER      se.ER      cv.ER
#> 1      1 1040        1040    130  72  6 0.5538462 0.02926903 0.05284685
#> 2      2  640         640     80  52  5 0.6500000 0.08292740 0.12758061
#> 3  Total 1680        1680    210 124 11 0.5904762 0.03641856 0.06167659
#> 
#> Abundance:
#>   Label  Estimate       se         cv       lcl      ucl        df
#> 1     1 123.22977 11.75088 0.09535744 101.72724 149.2774 43.918771
#> 2     2  88.99928 13.37273 0.15025666  62.88926 125.9495  7.658528
#> 3 Total 212.22905 21.33324 0.10051991 173.30068 259.9019 40.063051
#> 
#> Density:
#>   Label  Estimate         se         cv        lcl       ucl        df
#> 1     1 0.1184902 0.01129892 0.09535744 0.09781465 0.1435359 43.918771
#> 2     2 0.1390614 0.02089490 0.15025666 0.09826447 0.1967961  7.658528
#> 3 Total 0.1263268 0.01269836 0.10051991 0.10315517 0.1547035 40.063051
#> 
#> Summary for individuals
#> 
#> Summary statistics:
#>   Region Area CoveredArea Effort   n  k       ER     se.ER      cv.ER mean.size
#> 1      1 1040        1040    130 229  6 1.761538 0.1165805 0.06618107  3.180556
#> 2      2  640         640     80 152  5 1.900000 0.3342319 0.17591151  2.923077
#> 3  Total 1680        1680    210 381 11 1.814286 0.1463570 0.08066920  3.072581
#>     se.mean
#> 1 0.2086982
#> 2 0.2261991
#> 3 0.1537082
#> 
#> Abundance:
#>   Label Estimate       se        cv      lcl      ucl        df
#> 1     1 391.9391 40.50494 0.1033450 317.2772 484.1706 27.423274
#> 2     2 260.1517 50.20666 0.1929899 162.2494 417.1289  5.786773
#> 3 Total 652.0909 73.79805 0.1131714 516.5938 823.1274 23.815556
#> 
#> Density:
#>   Label  Estimate         se        cv       lcl       ucl        df
#> 1     1 0.3768645 0.03894706 0.1033450 0.3050742 0.4655487 27.423274
#> 2     2 0.4064871 0.07844791 0.1929899 0.2535147 0.6517639  5.786773
#> 3 Total 0.3881493 0.04392741 0.1131714 0.3074963 0.4899568 23.815556
#> 
#> Expected cluster size
#>   Region Expected.S se.Expected.S cv.Expected.S
#> 1      1   3.180556     0.2114629    0.06648615
#> 2      2   2.923077     0.1750319    0.05987935
#> 3  Total   3.072581     0.1391365    0.04528327

# specify order 2 cosine adjustments
ds.model.cos2 <- ds(tee.data, 4, adjustment="cos", order=2)
#> Fitting half-normal key function with cosine(2) adjustments
#> AIC= 313.124
#> No survey area information supplied, only estimating detection function.
summary(ds.model.cos2)
#> 
#> Summary for distance analysis 
#> Number of observations :  124 
#> Distance range         :  0  -  4 
#> 
#> Model       : Half-normal key function with cosine adjustment term of order 2 
#> 
#> Strict monotonicity constraints were enforced.
#> AIC         :  313.1239 
#> Optimisation:  MCDS.exe 
#> 
#> Detection function parameters
#> Scale coefficient(s):  
#>              estimate        se
#> (Intercept) 0.6606793 0.1043329
#> 
#> Adjustment term coefficient(s):  
#>                 estimate        se
#> cos, order 2 -0.01593329 0.1351281
#> 
#>                        Estimate          SE        CV
#> Average p             0.5925864  0.08165162 0.1377885
#> N in covered region 209.2521718 31.22787931 0.1492356

# specify order 2 and 3 cosine adjustments, turning monotonicity
# constraints off
ds.model.cos23 <- ds(tee.data, 4, adjustment="cos", order=c(2, 3),
                   monotonicity=FALSE)
#> Fitting half-normal key function with cosine(2,3) adjustments
#> AIC= 314.26
#> No survey area information supplied, only estimating detection function.
# check for non-monotonicity -- actually no problems
check.mono(ds.model.cos23$ddf, plot=TRUE, n.pts=100)

#> [1] TRUE

# include both a covariate and adjustment terms in the model
ds.model.cos2.sex <- ds(tee.data, 4, adjustment="cos", order=2,
                        monotonicity=FALSE, formula=~as.factor(sex))
#> Fitting half-normal key function with cosine(2) adjustments
#> Warning: Detection function is not weakly monotonic!
#> Warning: Detection function is not strictly monotonic!
#> Warning: Detection function is greater than 1 at some distances
#> Warning: Detection function is not weakly monotonic!
#> Warning: Detection function is not strictly monotonic!
#> Warning: Detection function is greater than 1 at some distances
#> AIC= 306.019
#> Warning: Detection function is not weakly monotonic!
#> Warning: Detection function is not strictly monotonic!
#> Warning: Detection function is greater than 1 at some distances
#> No survey area information supplied, only estimating detection function.
# check for non-monotonicity -- actually no problems
check.mono(ds.model.cos2.sex$ddf, plot=TRUE, n.pts=100)
#> Warning: Detection function is not weakly monotonic!
#> Warning: Detection function is not strictly monotonic!
#> Warning: Detection function is greater than 1 at some distances

#> [1] FALSE

# truncate the largest 10% of the data and fit only a hazard-rate
# detection function
ds.model.hr.trunc <- ds(tee.data, truncation="10%", key="hr",
                        adjustment=NULL)
#> Fitting hazard-rate key function
#> Warning: Estimated hazard-rate scale parameter close to 0 (on log scale). Possible problem in data (e.g., spike near zero distance).
#> Warning: Estimated hazard-rate scale parameter close to 0 (on log scale). Possible problem in data (e.g., spike near zero distance).
#> AIC= 260.267
#> Warning: Estimated hazard-rate scale parameter close to 0 (on log scale). Possible problem in data (e.g., spike near zero distance).
#> No survey area information supplied, only estimating detection function.
summary(ds.model.hr.trunc)
#> 
#> Summary for distance analysis 
#> Number of observations :  117 
#> Distance range         :  0  -  3.104 
#> 
#> Model       : Hazard-rate key function 
#> AIC         :  260.2669 
#> Optimisation:  mrds (nlminb) 
#> 
#> Detection function parameters
#> Scale coefficient(s):  
#>              estimate        se
#> (Intercept) 0.5240633 0.4245238
#> 
#> Shape coefficient(s):  
#>             estimate       se
#> (Intercept)        0 0.594522
#> 
#>                        Estimate         SE        CV
#> Average p             0.6969118  0.1182424 0.1696662
#> N in covered region 167.8835155 29.7381876 0.1771358

# compare AICs between these models:
AIC(ds.model)
#>          df      AIC
#> ds.model  1 311.1385
AIC(ds.model.cos2)
#>               df      AIC
#> ds.model.cos2  2 313.1239
AIC(ds.model.cos23)
#>                df      AIC
#> ds.model.cos23  3 314.2601