Alternative optimization engine for fitting detection functions
Len Thomas
CREEM, Univ of St AndrewsSeptember 2025
Source:vignettes/web-only/alt-optimise/mcds-dot-exe.Rmd
mcds-dot-exe.RmdHere we demonstrate the use of the alternative optimization engine mcds.exe in the Distance and mrds packages. This engine was introduced with Distance version 1.0.8 and mrds version 2.2.9 to provide an alternative to the built-in optimizer in our R packages – but subsequent improvements in the built-in optimizer implemented in Distance 2.0.0 and mrds 3.0.0 mean that we no longer recommend use of mcds.exe. Nevertheless, the option to use mcds.exe remains open, and may be useful for some users, so we have retained this vignette. We may deprecate the option in future releases.
Note also that this vignette is designed for use within the Microsoft Windows operating system – the mcds.exe engine only has experimental support for MacOS or Linux (see the MCDS.exe help page within the mrds package.for more information).
Objectives
- Download the mcds.exe optimization engine
- Demonstrate its use in a simple line transect example (golf tee dataset) via the
Distancepackage - Demonstrate the same example via the
mrdspackage - Demonstrate its use in a point transect example (wren data) where one of the optimizers does not work well (gives a negative estimated detection probability)
- Demonstrate its use to speed up an analysis of camera trap distance sampling data (duiker data) via the
Distancepackage - Discuss when using the alternative optimization engine may be useful.
Introduction
The Distance package is designed to provide a simple way to fit detection functions and estimate abundance using conventional distance sampling methodology (i.e., single observer distance sampling, possibly with covariates, as described by Buckland et al. (2015)). The main function is ds. Underlying Distance is the package mrds – when the function ds is called it does some pre-processing and then calls the function ddf in the mrds package to do the work of detection function fitting. mrds uses maximum likelihood to fit the specified detection function model to the distance data using a built-in algorithm written in R.
An alternative method for analyzing distance sampling data is using the Distance for Windows software (Thomas et al., 2010). This software also uses maximum liklihood to fit the detection function models, and relies on software written in the programming language FORTRAN to do the fitting. The filename of this software is MCDS.exe.
In a perfect world, both methods would produce identical results given the same data and model specification, since the likelihood has only one maximum. However, the likelihood surface is sometimes complex, especially when monotonicity constraints are used (which ensures the estimated detection probability is flat or decreasing with increasing distance when adjustment terms are used) or with “overdispersed” or “spiked” data (see Figure 2 in Thomas et al. (2010)), and so in some (rare) cases one or other piece of software fails to find the maximum. Note that in our tests, we have found this to be extremely rare from Distance version 2.0.0 and mrds version 3.0.0 onwards. Nevertheless, to counteract this, it is possible to run both the R-based optimizer and MCDS.exe from the ds function within the Distance package or the ddf function within mrds package.
Another historical motivation for using the MCDS.exe software from within R was that the R-based optimizer was sometimes slow to converge and so using MCDS.exe in place of the R-based optimizer can then save significant time, particularly when doing a nonparametric bootstrap for large datasets. However, from Distance 2.0.0 and mrds 3.0.0 the R-based optimizer is no longer generally slower.
This vignette demonstrates how to download and then use the MCDS.exe software from within the Distance and mrds packages. For more information, see the MCDS.exe help page within the mrds package.
Downloading and verifying MCDS.exe
The program MCDS.exe does not come automatically with the Distance or mrds packages, to avoid violating CRAN rules, so you must first download it from the distance sampling website.
#Unload Distance package if it's already loaded in R
if("Distance" %in% (.packages())){
detach("package:Distance", unload=TRUE)
}
#Download MCDS.exe
download.file("http://distancesampling.org/R/MCDS.exe", paste0(system.file(package="mrds"),"/MCDS.exe"), mode = "wb")
#Load the Distance package - now it will be able to use MCDS.exe
library(Distance)## Loading required package: mrds## This is mrds 3.0.1
## Built: R 4.5.1; ; 2025-07-06 23:50:32 UTC; windows##
## Attaching package: 'Distance'## The following object is masked from 'package:mrds':
##
## create.binsNow that this software is available, both it and the R optimizer will be used by default for each analysis; you can also choose to use just one or the other, as shown below.
Example with Golf Tee data
Both MCDS.exe and the R-based optimizer
This example (of golf tee data, using only observer 1) is taken from the R help for the ds function: (There is a warning about cluster sizes being coded as -1 that can be ignored.)
#Load data
data(book.tee.data)
tee.data <- subset(book.tee.data$book.tee.dataframe, observer==1)
#Fit detection function - default is half-normal with cosine adjustments
ds.model <- ds(tee.data, truncation = 4)## Starting AIC adjustment term selection.## Fitting half-normal key function## AIC= 311.138## Fitting half-normal key function with cosine(2) adjustments## AIC= 313.124##
## Half-normal key function selected.## No survey area information supplied, only estimating detection function.
summary(ds.model)##
## Summary for distance analysis
## Number of observations : 124
## Distance range : 0 - 4
##
## Model : Half-normal key function
## AIC : 311.1385
## Optimisation: mrds (nlminb)
##
## Detection function parameters
## Scale coefficient(s):
## estimate se
## (Intercept) 0.6632435 0.09981249
##
## Estimate SE CV
## Average p 0.5842744 0.04637627 0.07937412
## N in covered region 212.2290462 20.85130344 0.09824906Assuming you have MCDS.exe installed, the default is that both it and the R-based optimizer are run. Both give the same result in this example, and when this happens the result from the R-based optimizer is used. You can see this from the line of summary output:
Optimisation: mrds (nlminb)
where mrds is the R package that the Distance package relies on, and nlminb is the R-based optimizer.
You can see the process of both optimizers being used by setting the debug_level argument of the ds function to a value larger than the default of 0 and then examining the output:
ds.model <- ds(tee.data, truncation = 4, debug_level = 1)## Starting AIC adjustment term selection.## Fitting half-normal key function## DEBUG: initial values = -0.1031529## Running MCDS.exe...## Command file written to C:\Users\erexs\AppData\Local\Temp\Rtmp4kuvHu\cmdtmp245c6a52373d.txt## Stats file written to C:\Users\erexs\AppData\Local\Temp\Rtmp4kuvHu\stat245c2e9e93.txt## DEBUG: initial values = 0.6632378
##
## DEBUG: Convergence!
## Iteration 0.0
## Converge = 0
## nll = 154.5692
## parameters = 0.6632378## MCDS.exe log likehood: -154.5697## MCDS.exe pars: 1.941067## mrds refitted log likehood: -154.5692276## mrds refitted pars: 0.6632378##
## DEBUG: Convergence!
## Iteration 0.0
## Converge = 0
## nll = 154.5692
## parameters = 0.6632435## AIC= 311.138## Fitting half-normal key function with cosine(2) adjustments## DEBUG: initial values = -0.1031529 0## Running MCDS.exe...## Command file written to C:\Users\erexs\AppData\Local\Temp\Rtmp4kuvHu\cmdtmp245c7817759e.txt## Stats file written to C:\Users\erexs\AppData\Local\Temp\Rtmp4kuvHu\stat245c6a81318f.txt## DEBUG: initial values = 0.6606793 -0.0159333
##
## DEBUG: Convergence!
## Iteration 0.0
## Converge = 0
## nll = 154.5619
## parameters = 0.6606793, -0.0159333## MCDS.exe log likehood: -154.5624## MCDS.exe pars: 1.936107, -0.0159333## mrds refitted log likehood: -154.5619307## mrds refitted pars: 0.6606793, -0.0159333## iteration: 1
## f(x) = 243.539291
## iteration: 2
## f(x) = 164.079444
## iteration: 3
## f(x) = 156.273060
## iteration: 4
## f(x) = 155.340034
## iteration: 5
## f(x) = 154.684098
## iteration: 6
## f(x) = 154.571590
## iteration: 7
## f(x) = 154.562292
## iteration: 8
## f(x) = 154.561975
## iteration: 9
## f(x) = 154.561931
##
## DEBUG: Convergence!
## Iteration 0.0
## Converge = 0
## nll = 154.5619
## parameters = 0.6606883, -0.0159336
## DEBUG: MCDS lnl = -154.5619 mrds lnl = 154.5619## AIC= 313.124##
## Half-normal key function selected.## No survey area information supplied, only estimating detection function.First the half-normal with no adjustments is run; for this model the MCDS.exe software is run first, followed by the R-based (mrds) optimizer. Both converge and both give the same nll (negative log-likelihood) or 154.5692, giving an AIC of 311.138. The model with half-normal and a cosine adjustment of order 2 is then fitted to the data, with first the MCDS.exe optimizer and then the R-based optimizer. Again both give the same result of nll 154.5619 and an AIC of 313.124. This is higher than the AIC with no adjustments so half-normal with no adjustments is chosen.
In this case, both optimizers produced the same result, so there is no benefit to run MCDS.exe.
Specifying which optimzier to run
As we said earlier, the default behaviour when MCDS.exe has been downloaded is to run both MCDS.exe and the R-based optimizer. However, the optimizer argument can be used to specify which to use – either both, R or MCDS. Here is an example with just the MCDS.exe optimizer:
ds.model <- ds(tee.data, truncation = 4, optimizer = "MCDS")## Starting AIC adjustment term selection.## Fitting half-normal key function## AIC= 311.138## Fitting half-normal key function with cosine(2) adjustments## AIC= 313.124##
## Half-normal key function selected.## No survey area information supplied, only estimating detection function.
summary(ds.model)##
## Summary for distance analysis
## Number of observations : 124
## Distance range : 0 - 4
##
## Model : Half-normal key function
## AIC : 311.1385
## Optimisation: MCDS.exe
##
## Detection function parameters
## Scale coefficient(s):
## estimate se
## (Intercept) 0.6632378 0.09981136
##
## Estimate SE CV
## Average p 0.5842718 0.04637577 0.07937362
## N in covered region 212.2300013 20.85133459 0.09824876The summary output now says Optimisation: MCDS.exe.
Demonstration using ddf in mrds package
Here we demonstrate using both optimizers in the ddf function, rather than via ds.
#Half normal detection function
ddf.model <- ddf(dsmodel = ~mcds(key = "hn", formula = ~1), data = tee.data, method = "ds",
meta.data = list(width = 4))
#Half normal with cos(2) adjustment
ddf.model.cos2 <- ddf(dsmodel = ~mcds(key = "hn", adj.series = "cos", adj.order = 2, formula = ~1),
data = tee.data, method = "ds", meta.data = list(width = 4))
#Compare with AIC
AIC(ddf.model, ddf.model.cos2)## df AIC
## ddf.model 1 311.1385
## ddf.model.cos2 2 313.1239
#Model with no adjustment term has lower AIC; show summary of this model
summary(ddf.model)##
## Summary for ds object
## Number of observations : 124
## Distance range : 0 - 4
## AIC : 311.1385
## Optimisation : mrds (nlminb)
##
## Detection function:
## Half-normal key function
##
## Detection function parameters
## Scale coefficient(s):
## estimate se
## (Intercept) 0.6632435 0.09981249
##
## Estimate SE CV
## Average p 0.5842744 0.04637627 0.07937412
## N in covered region 212.2290462 20.85130344 0.09824906As an exercise, fit using just the MCDS.exe optimizer:
ddf.model <- ddf(dsmodel = ~mcds(key = "hn", adj.series = "cos", adj.order = 2,
formula = ~1), data = tee.data, method = "ds",
meta.data = list(width = 4),
control = list(optimizer = "MCDS"))
summary(ddf.model)##
## Summary for ds object
## Number of observations : 124
## Distance range : 0 - 4
## AIC : 313.1239
## Optimisation : MCDS.exe
##
## Detection function:
## Half-normal key function with cosine adjustment term of order 2
##
## Detection function parameters
## Scale coefficient(s):
## estimate se
## (Intercept) 0.6606782 0.1043327
##
## Adjustment term coefficient(s):
## estimate se
## cos, order 2 -0.01593274 0.1351281
##
## Estimate SE CV
## Average p 0.5925856 0.08165144 0.1377884
## N in covered region 209.2524623 31.22790760 0.1492356Point transect example - wren data
This is an example of point transect data for a bird (wren), from Buckland (2006). In this case one of the optimizers fails correctly to constrain the detection function so the probability of detection is more than zero at all distances, and so we use the other optimizer for inference.
We load the wren 5 minute example dataset and define cutpoints for the distances (they were collected in intervals).
The following call to ds gives several warnings. Some warnings are about the detection function being less than zero at some distances. There is also a warning about the Hessian (which is used for variance estimation), but this relates to the Hermite(4, 6) model (i.e., two Hermite adjustment terms of order 4 and 6) which is not chosen using AIC and so this warning can be ignored.
wren5min.hn.herm.t100 <- ds(data = wren_5min, key = "hn", adjustment = "herm",
transect = "point", cutpoints = bin.cutpoints.100m)## Warning in create_bins(data, cutpoints): Some distances were outside bins and
## have been removed.## Starting AIC adjustment term selection.## Fitting half-normal key function## AIC= 427.471## Fitting half-normal key function with Hermite(4) adjustments## Warning in check.mono(result, n.pts = control$mono.points): Detection function
## is less than 0 at some distances## Warning in check.mono(result, n.pts = control$mono.points): Detection function
## is less than 0 at some distances## AIC= 422.228## Fitting half-normal key function with Hermite(4,6) adjustments## Warning: First partial hessian is singular and second-partial hessian is NULL, no hessian
## Warning: Detection function is less than 0 at some distances
## Warning: Detection function is less than 0 at some distances## AIC= 423.255##
## Half-normal key function with Hermite(4) adjustments selected.## Warning in mrds::check.mono(model, n.pts = 10): Detection function is less than
## 0 at some distances
summary(wren5min.hn.herm.t100)##
## Summary for distance analysis
## Number of observations : 132
## Distance range : 0 - 100
##
## Model : Half-normal key function with Hermite polynomial adjustment term of order 4
##
## Strict monotonicity constraints were enforced.
## AIC : 422.2284
## Optimisation: MCDS.exe
##
## Detection function parameters
## Scale coefficient(s):
## estimate se
## (Intercept) 12.08697 1e+05
##
## Adjustment term coefficient(s):
## estimate se
## herm, order 4 0.5723854 0.07888508
##
## Estimate SE CV
## Average p 0.4399177 0.0253475 0.05761875
## N in covered region 300.0561563 26.0944820 0.08696533
##
## Summary statistics:
## Region Area CoveredArea Effort n k ER se.ER cv.ER
## 1 Montrave 33.2 2010619 64 132 32 2.0625 0.1901692 0.09220324
##
## Abundance:
## Label Estimate se cv lcl ucl df
## 1 Total 0.004954625 0.0005386969 0.1087261 0.003988075 0.006155428 57.83608
##
## Density:
## Label Estimate se cv lcl ucl df
## 1 Total 0.0001492357 1.622581e-05 0.1087261 0.0001201227 0.0001854045 57.83608The MCDS.exe optimizer is the chosen one (see the `Optimisation’ line of output).
The warnings persist if only the MCDS.exe optimizer is used:
wren5min.hn.herm.t100.mcds <- ds(data = wren_5min, key = "hn", adjustment = "herm",
transect = "point", cutpoints = bin.cutpoints.100m,
optimizer = "MCDS")## Warning in create_bins(data, cutpoints): Some distances were outside bins and
## have been removed.## Starting AIC adjustment term selection.## Fitting half-normal key function## AIC= 427.471## Fitting half-normal key function with Hermite(4) adjustments## Warning in check.mono(result, n.pts = control$mono.points): Detection function
## is less than 0 at some distances## Warning in check.mono(result, n.pts = control$mono.points): Detection function
## is less than 0 at some distances## AIC= 422.228## Fitting half-normal key function with Hermite(4,6) adjustments## Warning: First partial hessian is singular and second-partial hessian is NULL, no hessian
## Warning: Detection function is less than 0 at some distances
## Warning: Detection function is less than 0 at some distances## AIC= 423.255##
## Half-normal key function with Hermite(4) adjustments selected.## Warning in mrds::check.mono(model, n.pts = 10): Detection function is less than
## 0 at some distancesLooking at a plot of the fitted object (Figure 1), it seems that the evaluated pdf is less than 0 at distances close to the truncation point (approx. 95m and greater):
plot(wren5min.hn.herm.t100.mcds, pdf = TRUE)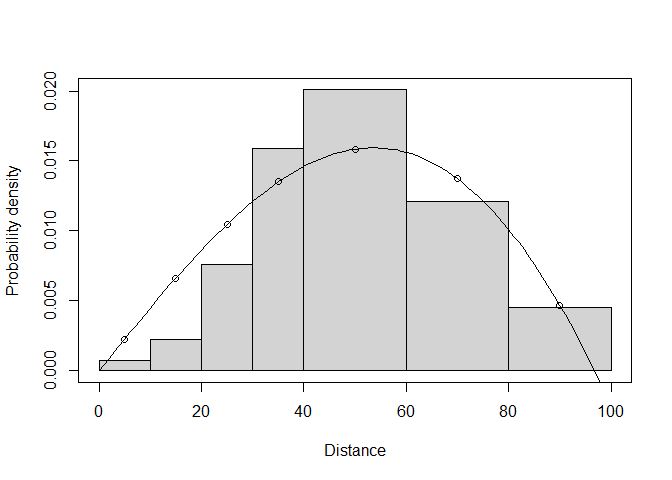
Figure 1: PDF of fitted model with MCDS optimizer.
What appears to be happening here is a failure of the optimization routine to appropriately constrain the model parameters so that the detection function is valid. This happens on occasion (the routines aren’t perfect!) and where it does we recommend trying the other optimization routine. Here we use the R-based optimizer:
wren5min.hn.herm.t100.r <- ds(data=wren_5min, key="hn", adjustment="herm",
transect="point", cutpoints=bin.cutpoints.100m,
optimizer = "R")## Warning in create_bins(data, cutpoints): Some distances were outside bins and
## have been removed.## Starting AIC adjustment term selection.## Fitting half-normal key function## AIC= 427.471## Fitting half-normal key function with Hermite(4) adjustments## AIC= 422.73## Fitting half-normal key function with Hermite(4,6) adjustments## AIC= 424.717##
## Half-normal key function with Hermite(4) adjustments selected.Here the fitted AIC for the chosen model (half normal with one Hermite adjustment of order 4) is 422.73, higher than that with the MCDS.exe optimizer (which was 422.23), which explains why the MCDS.exe optimizer fit was chosen when we allowed ds to choose freely. However, the detection function fit from MCDS.exe was invalid, because it went lower than 0 at about 95m, while the fit with the R-based optimizer looks valid (Figure 2):
plot(wren5min.hn.herm.t100.r, pdf = TRUE)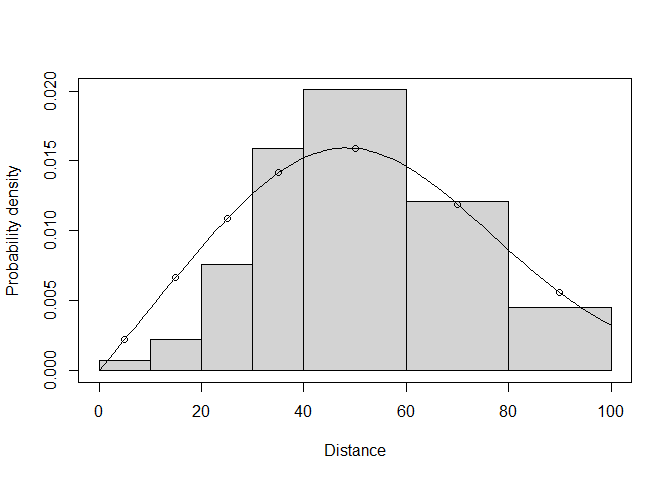
Figure 2: PDF of fitted model with R-based optimizer.
Hence in this case, we would use the R-based optimizer’s fit.
Camera trap example
For this example, it helps if you are familiar with the Analysis of camera trapping data vignette on the distance sampling web site.
You also need to Download from the Dryad data repository the detection distances for the full daytime data set and then read it in with the code below:
#Read in data and set up data for analysis
DuikerCameraTraps <- read.csv(file="DaytimeDistances.txt", header=TRUE, sep="\t")
DuikerCameraTraps$Area <- DuikerCameraTraps$Area / (1000*1000)
DuikerCameraTraps$object <- NA
DuikerCameraTraps$object[!is.na(DuikerCameraTraps$distance)] <- 1:sum(!is.na(DuikerCameraTraps$distance))
#Specify breakpoints and truncation
trunc.list <- list(left=2, right=15)
mybreaks <- c(seq(2, 8, 1), 10, 12, 15)Then we fit the detection function selected in the camera trap vignette, uniform plus 3 cosine adjustment terms, and time how long the fitting takes:
start.time <- Sys.time()
uni3.r <- ds(DuikerCameraTraps, transect = "point", key="unif", adjustment = "cos",
nadj=3, cutpoints = mybreaks, truncation = trunc.list, optimizer = "R")## Warning in create_bins(data, cutpoints): Some distances were outside bins and
## have been removed.## Fitting uniform key function with cosine(1,2,3) adjustments## AIC= 44012.238##
## Summary for distance analysis
## Number of observations : 10284
## Distance range : 2 - 15
##
## Model : Uniform key function with cosine adjustment terms of order 1,2,3
##
## Strict monotonicity constraints were enforced.
## AIC : 44012.24
## Optimisation: mrds (slsqp)
##
## Detection function parameters
## Scale coefficient(s):
## NULL
##
## Adjustment term coefficient(s):
## estimate se
## cos, order 1 0.93529846 0.01504415
## cos, order 2 -0.05342058 0.02438026
## cos, order 3 -0.08069257 0.01557680
##
## Estimate SE CV
## Average p 3.290022e-01 1.349494e-02 0.04101777
## N in covered region 3.125815e+04 1.306764e+03 0.04180555
##
## Summary statistics:
## Region Area CoveredArea Effort n k ER se.ER cv.ER
## 1 Tai 40.37 21858518573 31483179 10284 21 0.0003266506 8.763252e-05 0.268276
##
## Abundance:
## Label Estimate se cv lcl ucl df
## 1 Total 5.772996e-05 1.566754e-05 0.2713936 3.315829e-05 0.0001005103 20.94597
##
## Density:
## Label Estimate se cv lcl ucl df
## 1 Total 1.430021e-06 3.880986e-07 0.2713936 8.213597e-07 2.489727e-06 20.94597Fitting takes 9.6 secs. (Note, in versions of Distance before 2.0.0 this was a much higher number!) Here we try the MCDS.exe optimizer:
start.time <- Sys.time()
uni3.mcds <- ds(DuikerCameraTraps, transect = "point", key="unif", adjustment = "cos",
nadj=3, cutpoints = mybreaks, truncation = trunc.list, optimizer = "MCDS")## Warning in create_bins(data, cutpoints): Some distances were outside bins and
## have been removed.## Fitting uniform key function with cosine(1,2,3) adjustments## AIC= 44012.211##
## Summary for distance analysis
## Number of observations : 10284
## Distance range : 2 - 15
##
## Model : Uniform key function with cosine adjustment terms of order 1,2,3
##
## Strict monotonicity constraints were enforced.
## AIC : 44012.21
## Optimisation: MCDS.exe
##
## Detection function parameters
## Scale coefficient(s):
## NULL
##
## Adjustment term coefficient(s):
## estimate se
## cos, order 1 0.93518220 0.01504583
## cos, order 2 -0.05345965 0.02438049
## cos, order 3 -0.08073799 0.01557817
##
## Estimate SE CV
## Average p 3.290679e-01 1.349917e-02 0.04102246
## N in covered region 3.125191e+04 1.306645e+03 0.04181008
##
## Summary statistics:
## Region Area CoveredArea Effort n k ER se.ER cv.ER
## 1 Tai 40.37 21858518573 31483179 10284 21 0.0003266506 8.763252e-05 0.268276
##
## Abundance:
## Label Estimate se cv lcl ucl df
## 1 Total 5.771844e-05 1.566445e-05 0.2713943 3.315164e-05 0.0001004903 20.94619
##
## Density:
## Label Estimate se cv lcl ucl df
## 1 Total 1.429736e-06 3.880222e-07 0.2713943 8.21195e-07 2.489232e-06 20.94619This took a little less time: 8 secs. Hence, for some datasets, it may be quicker to use the MCDS.exe optimizer. This could make a significant difference if using the nonparametric bootstrap to estimate variance. However, after making improvements to the optimizer in mrds 3.0.0 and Distance 2.0.0 the difference is generally small, and in many cases the R optimizer is faster than MCDS.exe so this is likely not a productive avenue to pursue in general.
Discussion
We have shown how to fit distance sampling detection functions (for single platform data) using either the R-based optimizer built into the ddf function (via calling ddf or, more likely, calling the ds function in the Distance package) or the MCDS.exe analysis engine used by Distance for Windows. In the vast majority of cases both fitting methods give the same result, and so there is no need to use both. However, the only downside is that fitting takes longer, as each is called in turn. If you have downloaded the MCDS.exe file and want to speed things up, you can use just the R-based optimizer by specifying optimizer = "R" in the call to ds or ddf, or just the MCDS.exe optimizer with optimizer = "MCDS".
Some situations where the two may produce different results are given below. Note that in each case we give an update related to new algorithms developed and used in mrds 3.0.0.
-
Detection functions that are close to non-monotonic or close to zero at some distances. When adjustment terms are used in the detection function, then constraints are required to prevent the fitted function from having “bumps” where detection probability increases with increasing distance and also to prevent detection probability from becoming less than zero. The former are called monotonicity constraints and are set using the
monotonicityargument indsor in themeta.dataargument inddf; monotonicity is set on by default. In practice, monotonicity and values less than zero are monitored at a finite set of distances between the 0 and the right truncation point, and (for historical reasons) this set of distances is different for theR-based andMCDS.exeoptimizers. This typically makes no difference to the optimization, but particularly in borderline cases it can result in different fitted functions. Plotting the fitted functions (as we did in the wren example above) can reveal when there is an issue with a fitted function, and if this occurs the associated optimizer should not be used. In the future we plan to bring the two into line so they use the same distances for checking.- Update: As of
mrds3.0.0 andDistance2.0.0 these are now aligned, so this difference should have gone away.
- Update: As of
Detection functions with many adjustment terms. The two optimizers use different algorithms for optimization: the
R-based optimizer uses a routine callednlminbwhileMCDS.exeuses a nonlinear constrained optimizer routine produced by the IMSL group. In cases where there are multiple adjustment terms, and hence several parameters to estimate (that are often correlated) the likelihood maximization is harder, and one or other routine can sometimes fail to find the maximum. In this case, choosing the routine with the higher likelihood (i.e., lower negative log-likelihod, or equivalently lower AIC) is the right thing to do, and this is the default behaviour of the software.Update: in
mrds3.0.0 we now use a Sequential Least Squares Programming (SLSQP) algorithm from the ‘nloptr’ package vianlminbin theR-based optimizer (rather than the old solnp algorithm). The old algorithm can be accessed from theds() function inDistanceusing the argumentmono_method = "solnp"or with theddf() function inmrdsusing the argumentcontrol(mono.method = "solnp"). However, the new one shows improved performance in our testing, and so we do not recommend using the old algorithm except for reasons of backwards compatibility.Detection functions that are “overdispersed” or with a “spike” in the detection function close to zero distance. Similarly to the above, the detection function can then be hard to maximize and hence on or other optimizer can fail to find the maximum. Solution is as above. Overdispersed data is common in camera trap distance sampling because many detections can be generated by the same individual crossing in front of the camera.
Update is as above.
If you are interested in seeing more comparisons of the optimizers on various datasets, we maintain a test suite of both straightforward and challenging datasets together with test code to run and compare the two optimizers – this is available at the MCDS_mrds_compare repository.
If you encounter difficulties when using both optimizers, one possible troubleshooting step is to run the analysis first choosing one optimizer (e.g., specifing the argument optimizer = "MCDS") and then choosing the other (optimizer = "R"). This allows you clearly to see what the output of each optimizer is (including any error messages) and facilitates their comparison.
One other criterion to favour one optimizer over the other is speed. We found that for large datasets the MCDS.exe optimizer was quicker, but as of Distance 2.0.0 and mrds 3.0.0 this is no longer necessarily the case.
One thing to note is that the MCDS.exe file will get deleted each time you update the mrds package, so you’ll need to re-download the file if you want to continue using the MCDS.exe optimizer. As shown above, this only requires running one line of code.