Assessing line transect detection functions solution

Author

Centre for Research into Ecological and Environmental Modelling
University of St Andrews

Modified

November 2024

Solution

Assessing line transect detection functions

Fitting models to simulated data

library(Distance)
data("LTExercise")
head(LTExercise, n=3)
  Region.Label Area Sample.Label Effort object distance  Study.Area
1      Default    1       Line 1      5      1      7.9 LTExercise3
2      Default    1       Line 1      5      2     10.2 LTExercise3
3      Default    1       Line 1      5      3     12.4 LTExercise3

These data contain 105 observations. There were no detections on Line 11 and the format below indicates that NA is used to specify this.

LTExercise[100:102, ]
    Region.Label Area Sample.Label Effort object distance  Study.Area
100      Default    1      Line 10      7    100     16.6 LTExercise3
101      Default    1      Line 11      3     NA       NA LTExercise3
102      Default    1      Line 12      4    101      1.0 LTExercise3

Here we can see the effect of the different truncation options.

conversion.factor <- convert_units("meter", "kilometer", "square kilometer")
# Truncate at 20metres
lt.hn.t20m <- ds(data=LTExercise, key="hn", adjustment=NULL, truncation=20, 
                convert_units=conversion.factor)
summary(lt.hn.t20m)

Summary for distance analysis 
Number of observations :  103 
Distance range         :  0  -  20 

Model       : Half-normal key function 
AIC         :  599.4236 
Optimisation:  mrds (nlminb) 

Detection function parameters
Scale coefficient(s):  
            estimate        se
(Intercept) 2.388955 0.1176774

                       Estimate          SE         CV
Average p             0.6377021  0.05317053 0.08337832
N in covered region 161.5174244 16.52647650 0.10232008

Summary statistics:
   Region Area CoveredArea Effort   n  k       ER   se.ER     cv.ER
1 Default    1        1.92     48 103 12 2.145833 0.32184 0.1499837

Abundance:
  Label Estimate       se        cv      lcl      ucl       df
1 Total 84.12366 14.43574 0.1716014 58.86702 120.2166 18.65735

Density:
  Label Estimate       se        cv      lcl      ucl       df
1 Total 84.12366 14.43574 0.1716014 58.86702 120.2166 18.65735

This has excluded 2 observations.

lt.hn.t10per <- ds(data=LTExercise, key="hn", adjustment=NULL, truncation="10%", 
                convert_units=conversion.factor)
summary(lt.hn.t10per)

Summary for distance analysis 
Number of observations :  94 
Distance range         :  0  -  16.04 

Model       : Half-normal key function 
AIC         :  512.2441 
Optimisation:  mrds (nlminb) 

Detection function parameters
Scale coefficient(s):  
            estimate        se
(Intercept) 2.298481 0.1606186

                       Estimate          SE        CV
Average p             0.6946953  0.06767631 0.0974187
N in covered region 135.3111285 15.27178113 0.1128642

Summary statistics:
   Region Area CoveredArea Effort  n  k       ER    se.ER     cv.ER
1 Default    1     1.53984     48 94 12 1.958333 0.278492 0.1422087

Abundance:
  Label Estimate       se        cv      lcl      ucl       df
1 Total  87.8735 15.14734 0.1723767 61.68487 125.1806 23.14378

Density:
  Label Estimate       se        cv      lcl      ucl       df
1 Total  87.8735 15.14734 0.1723767 61.68487 125.1806 23.14378

This has excluded 11 observations. The plots are shown below.

plot(lt.hn.t20m, main="Truncation 20m")
plot(lt.hn.t10per, main="Truncation 10%")

Truncation at absolute distance

Truncation at relative distance

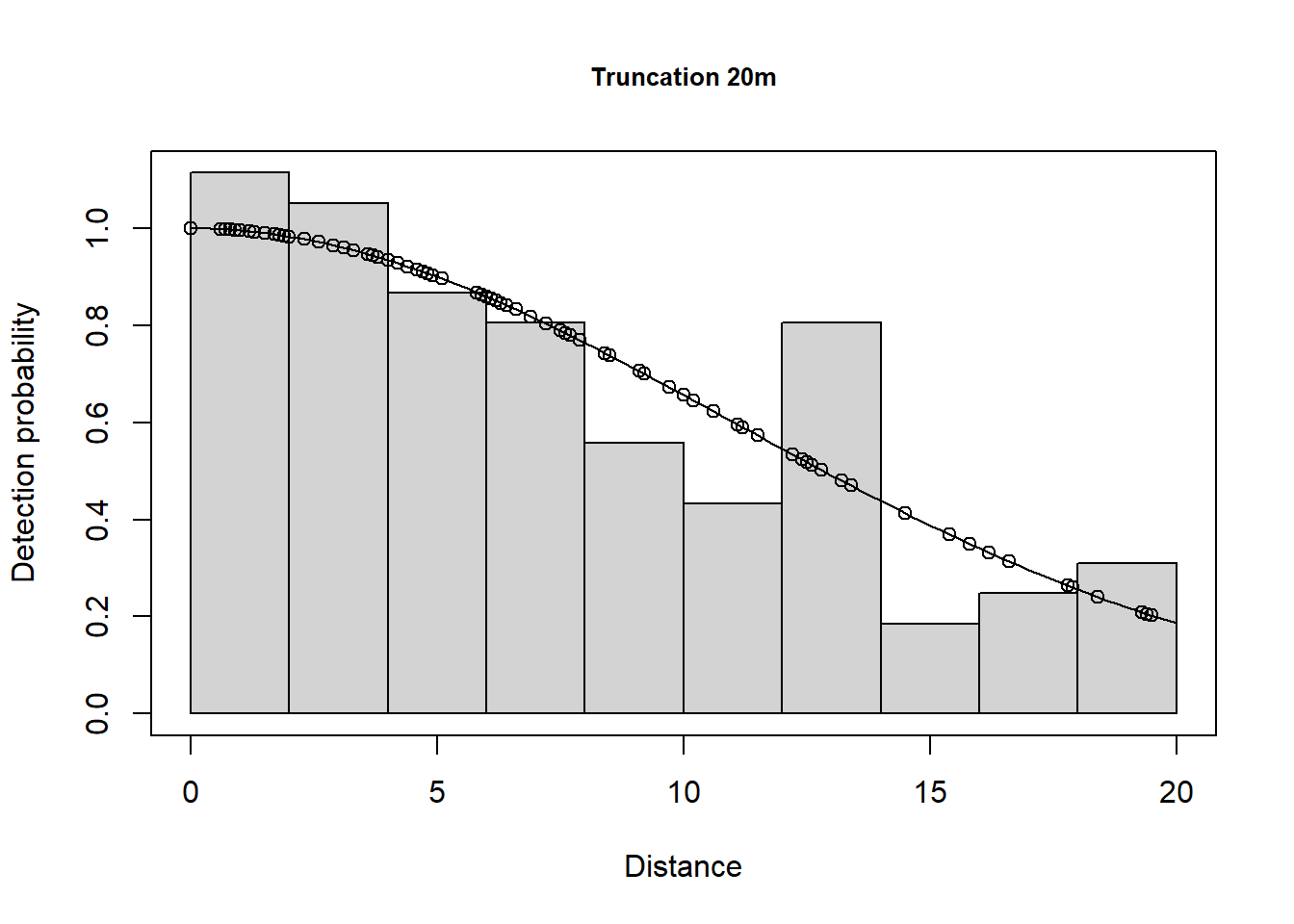
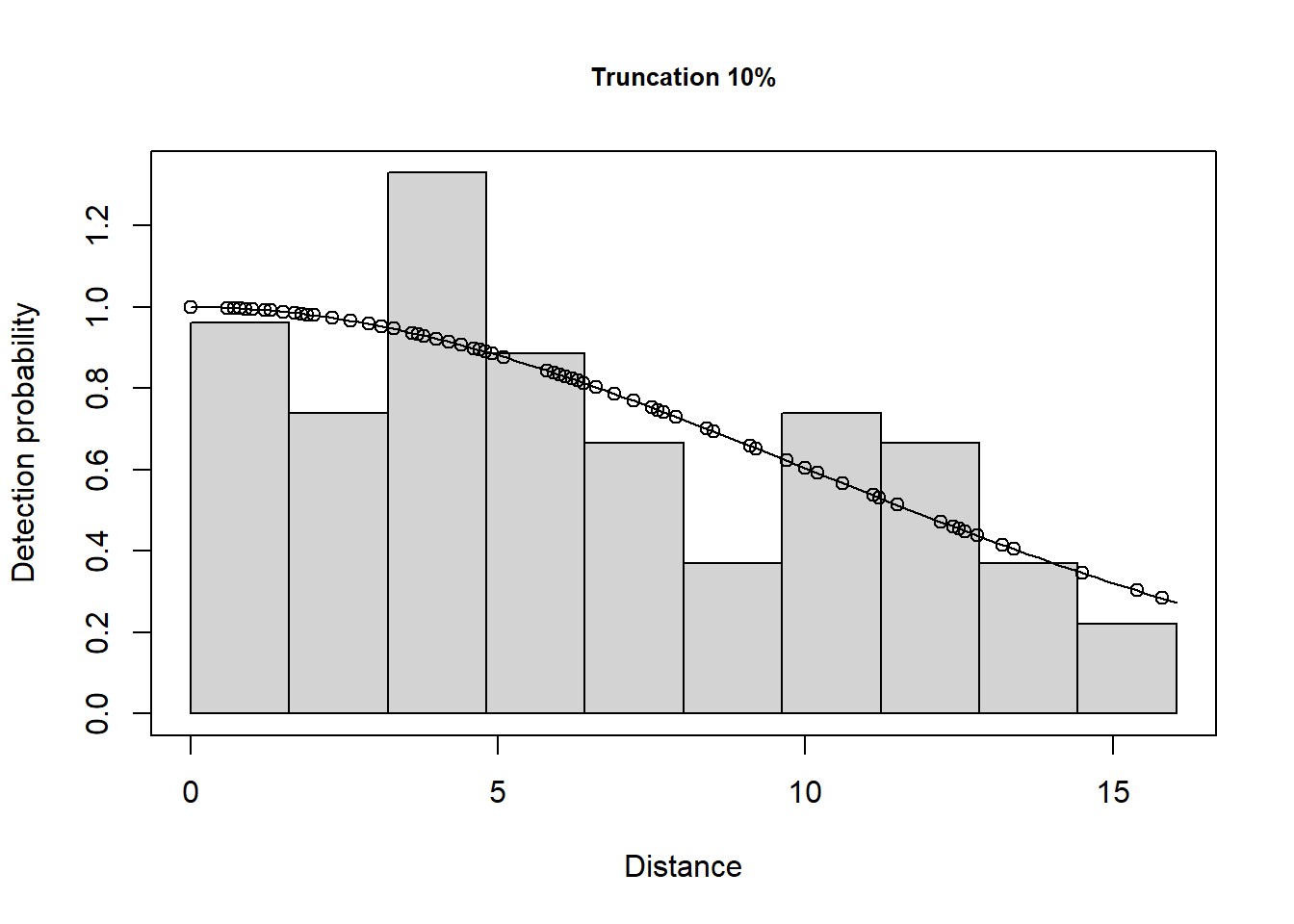
A few different models are shown below.

# Fit a few different models
# Half normal model, no adjustments, no truncation
lt.hn <- ds(data=LTExercise, key="hn", adjustment=NULL, convert_units=conversion.factor)
# Half normal model, cosine adjustments, truncation at 20m
lt.hn.cos.t20m <- ds(data=LTExercise, key="hn", adjustment="cos", truncation=20, 
                     convert_units=conversion.factor)
# Uniform model, cosine adjustments, truncation at 20m
lt.uf.cos.t20m <- ds(data=LTExercise, key="unif", adjustment="cos", 
                     truncation=20, convert_units=conversion.factor)
# Hazard rate model, no adjustments, truncation at 20m
lt.hr.t20m <- ds(data=LTExercise, key="hr", adjustment="poly", truncation=20,
                 convert_units=conversion.factor)

The results are shown in the table below: ‘Terms’ indicates the number of selected adjustment terms and ‘Pa’ is the estimated detection probability.

Results for simulated data with differing truncation and detection functions.
DetectionFunction Adjustments Terms Truncation AIC Pa Density D.CV Lower.CI Upper.CI
Half-normal None 0 35.8 636.936 0.349 87.494 0.158 62.703 122.086
Half-normal Cosine 0 20.0 599.424 0.638 84.124 0.172 58.867 120.217
Uniform Cosine 1 20.0 598.584 0.621 86.429 0.166 60.956 122.546
Hazard rate Polynomial 0 20.0 600.748 0.626 85.651 0.203 56.901 128.930

There is a change in \(\hat P_a\) due to truncation but all the models provide very similar density results, although precision is slightly poorer for the hazard rate model (because more parameters are estimated). Agreement between the estimate and the known true density is less good if you do not truncate the data, or do not truncate sufficiently. Note that the AIC values can only be compared for models with the same truncation and hence the same objects.

Take home message: with care, we can get reliable estimates using the wrong model (remember the data were simulated using a half normal detection function). It is gratifying because, in practise, the ‘correct’ model is never known.

plot(lt.hn, main="HN, no truncation")
plot(lt.hn.cos.t20m, main="HN, truncation at 20m")
plot(lt.uf.cos.t20m, main="Uniform, truncation at 20m")
plot(lt.hr.t20m, main="HR, truncation at 20m")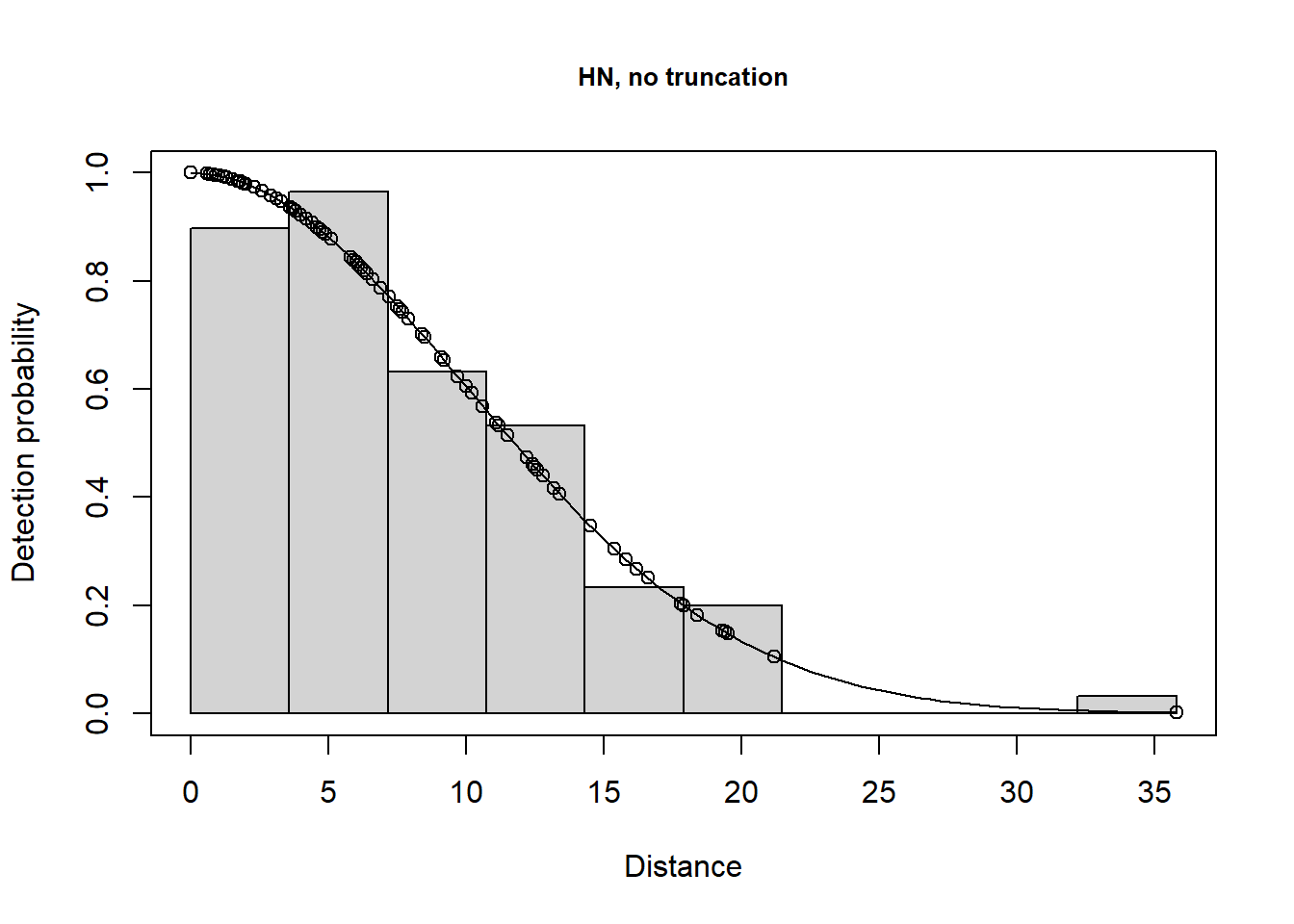

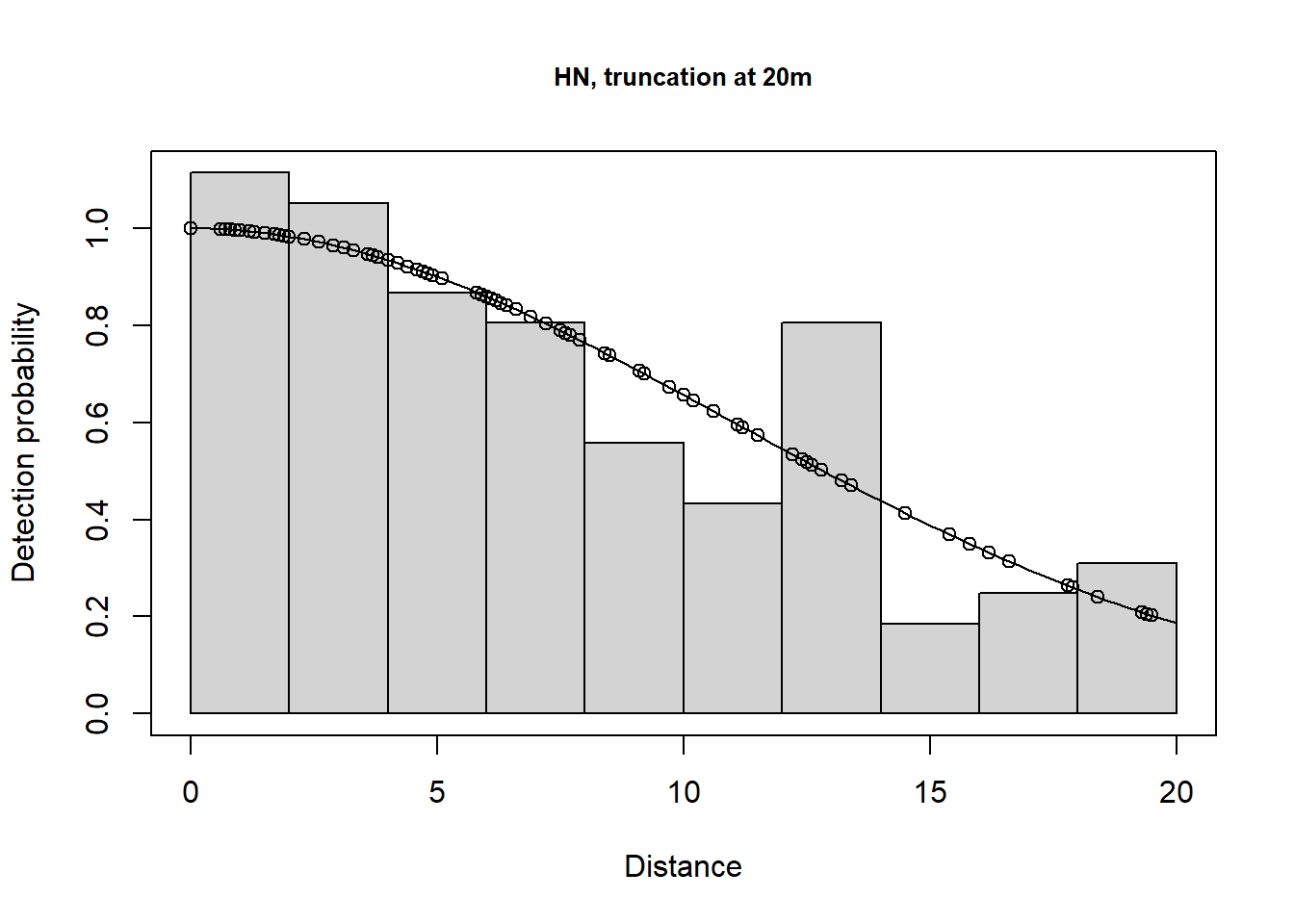
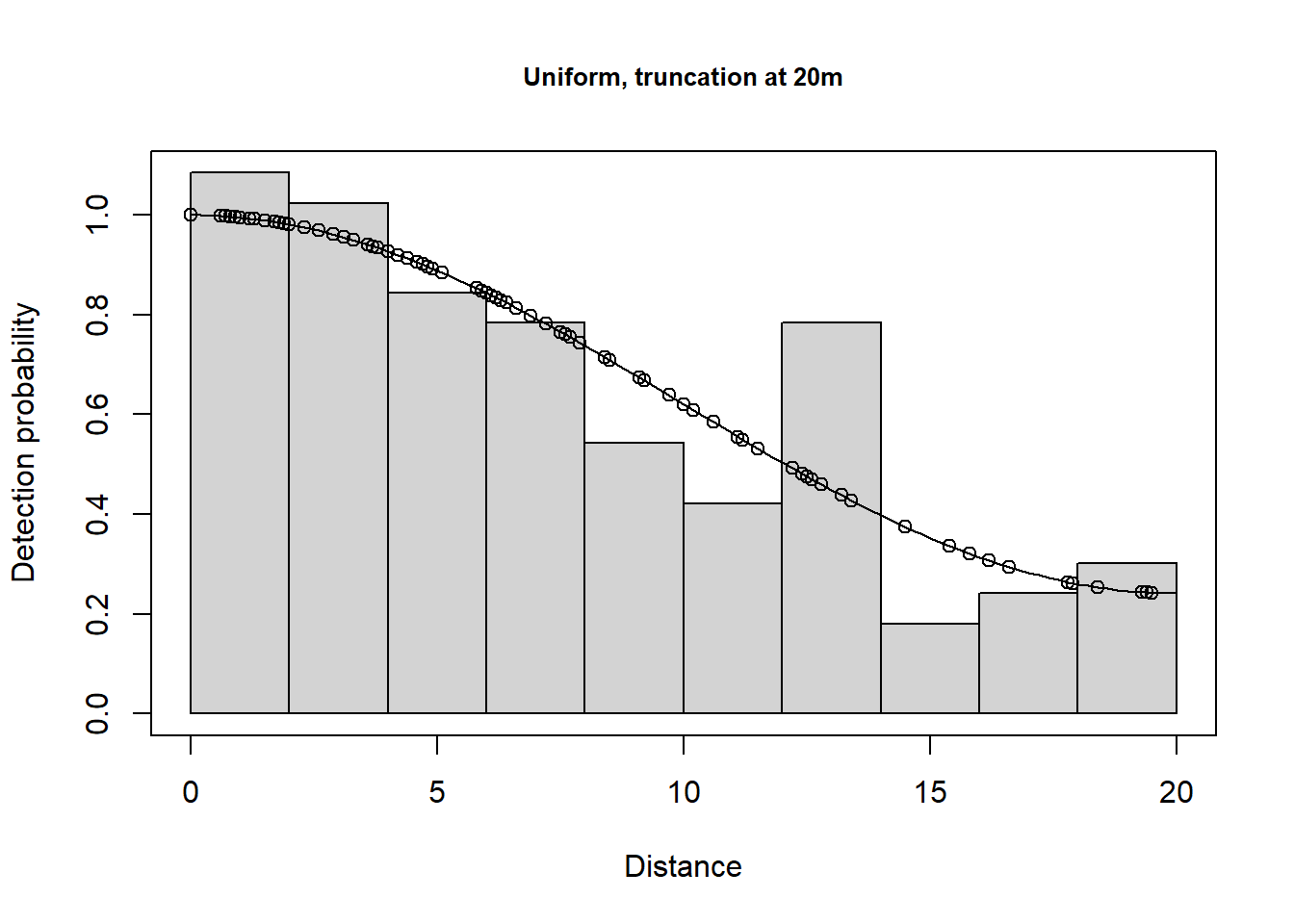
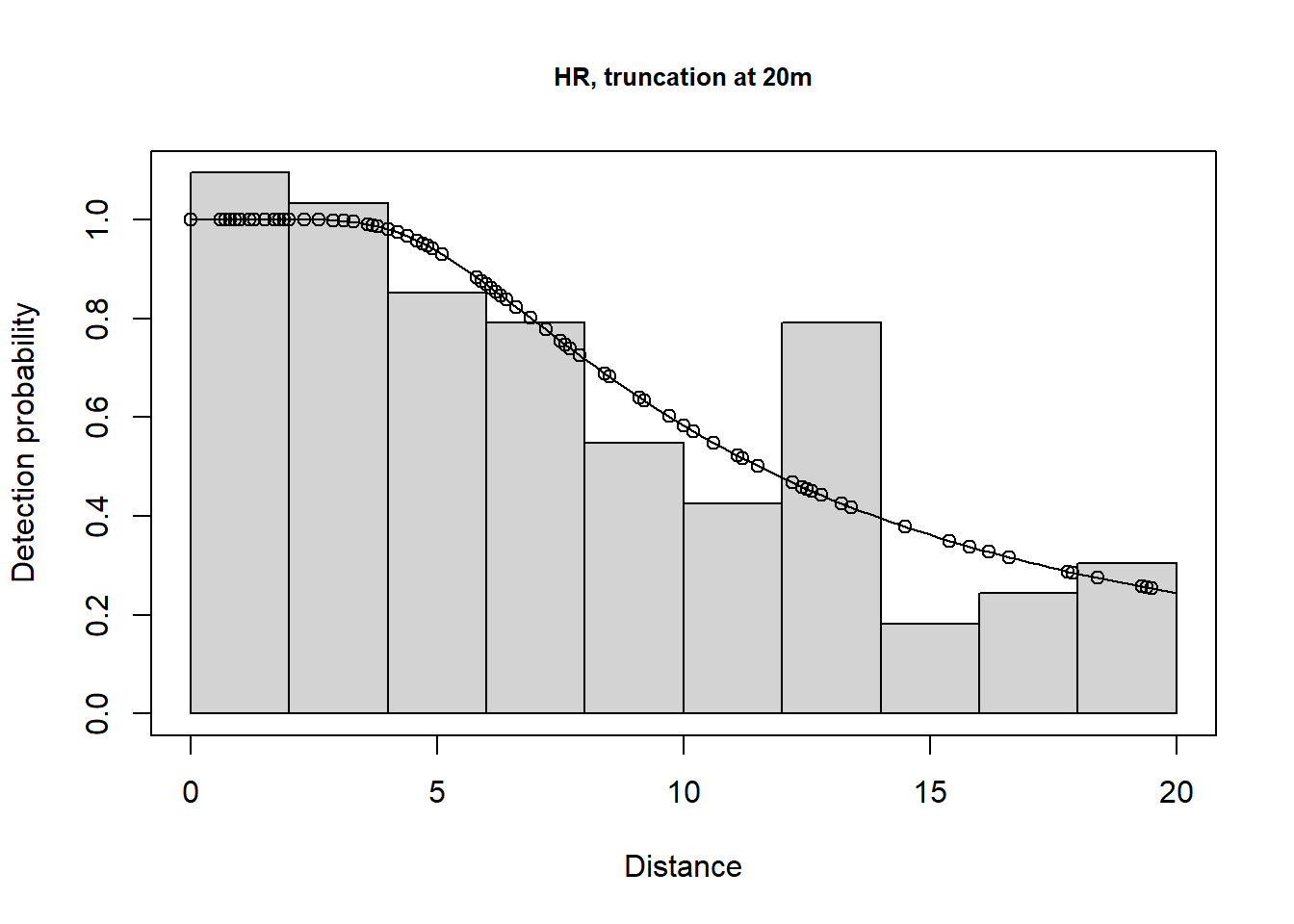
Half normal without truncation

Half normal 20m truncation

Uniform with adj 20m truncation

Hazard rate 20m truncation

Fitting models to real data (optional)

After accessing these data, a basic model is fitted and plotted to determine if truncation is required.

data(capercaillie)
knitr::kable(head(capercaillie, n=3))
Sample.Label Effort distance object size detected observer Region.Label Area
1 240 28 1 1 1 1 Monaughty Forest 1472
1 240 17 2 1 1 1 Monaughty Forest 1472
1 240 15 3 1 1 1 Monaughty Forest 1472 
conversion.factor <- convert_units("meter", "kilometer", "hectare")
# Fit a half normal model with no adjustments and no truncation
caper.hn <- ds(data=capercaillie, key="hn", adjustment=NULL, 
               convert_units=conversion.factor)
plot(caper.hn, nc=40)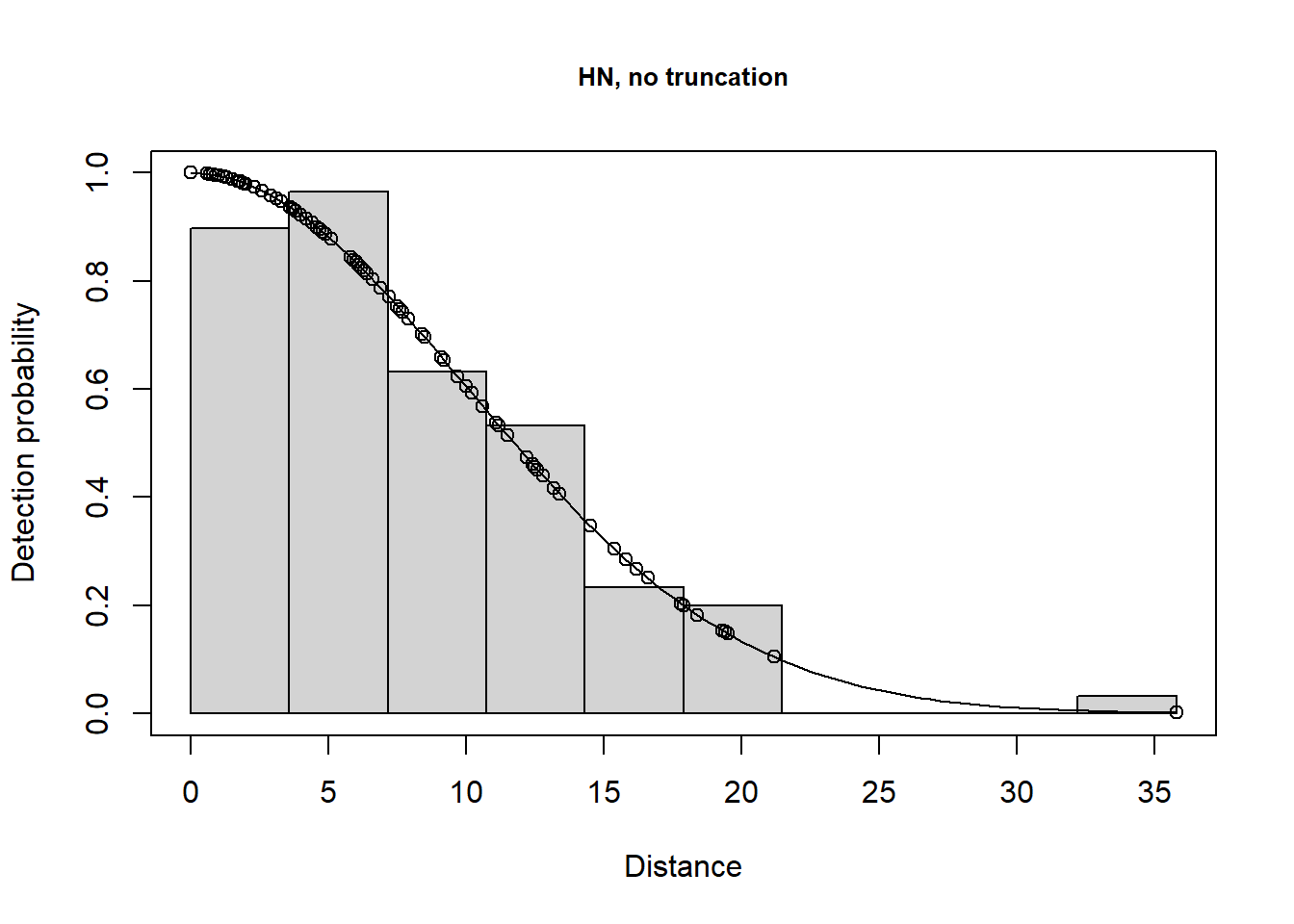

There is not a long tail to the histogram of perpendicular distances and so no truncation will be used.

There may be evidence of rounding to some values (e.g. 0, 30, 40, 70) however, we will ignore this at present (but address it below) and fit the three alternative key functions and use the default setting for adjustments terms (i.e. cosine up to order 5).

Fitting multiple models to exact distance data

# Half normal model 
caper.hn.cos <- ds(data=capercaillie, key="hn", adjustment="cos",
                   convert_units=conversion.factor)
# Hazard rate model  
caper.hr.cos <- ds(data=capercaillie, key="hr", adjustment="cos",
                   convert_units=conversion.factor)
# Uniform model  
caper.uf.cos <- ds(data=capercaillie, key="unif", adjustment="cos",
                   convert_units=conversion.factor)

The detection functions and QQ plots are shown below:

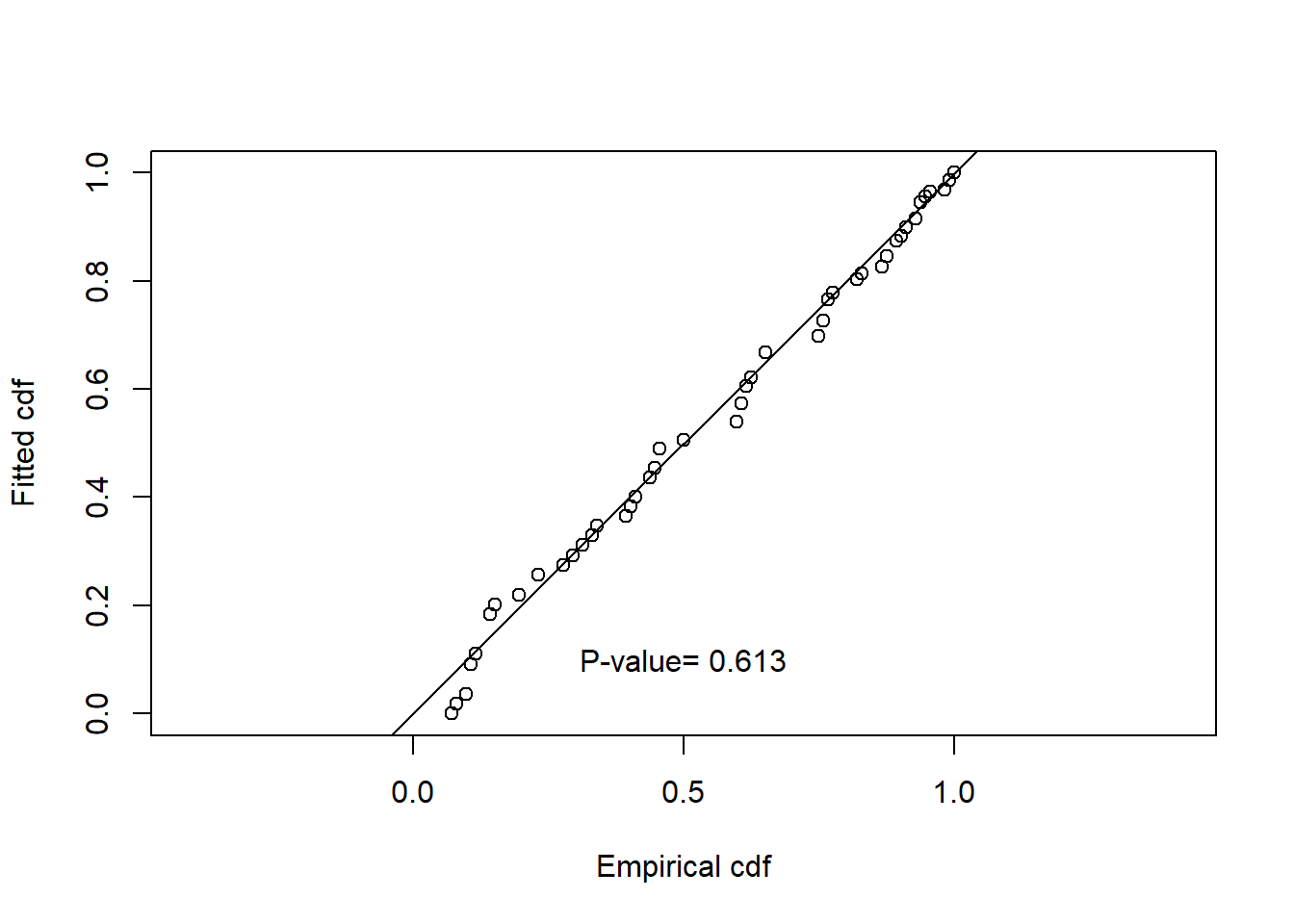
plot(caper.hn.cos, main="Half normal")
x <- gof_ds(caper.hn.cos)
text(.5, .1, paste("P-value=", round(x$dsgof$CvM$p,3)))
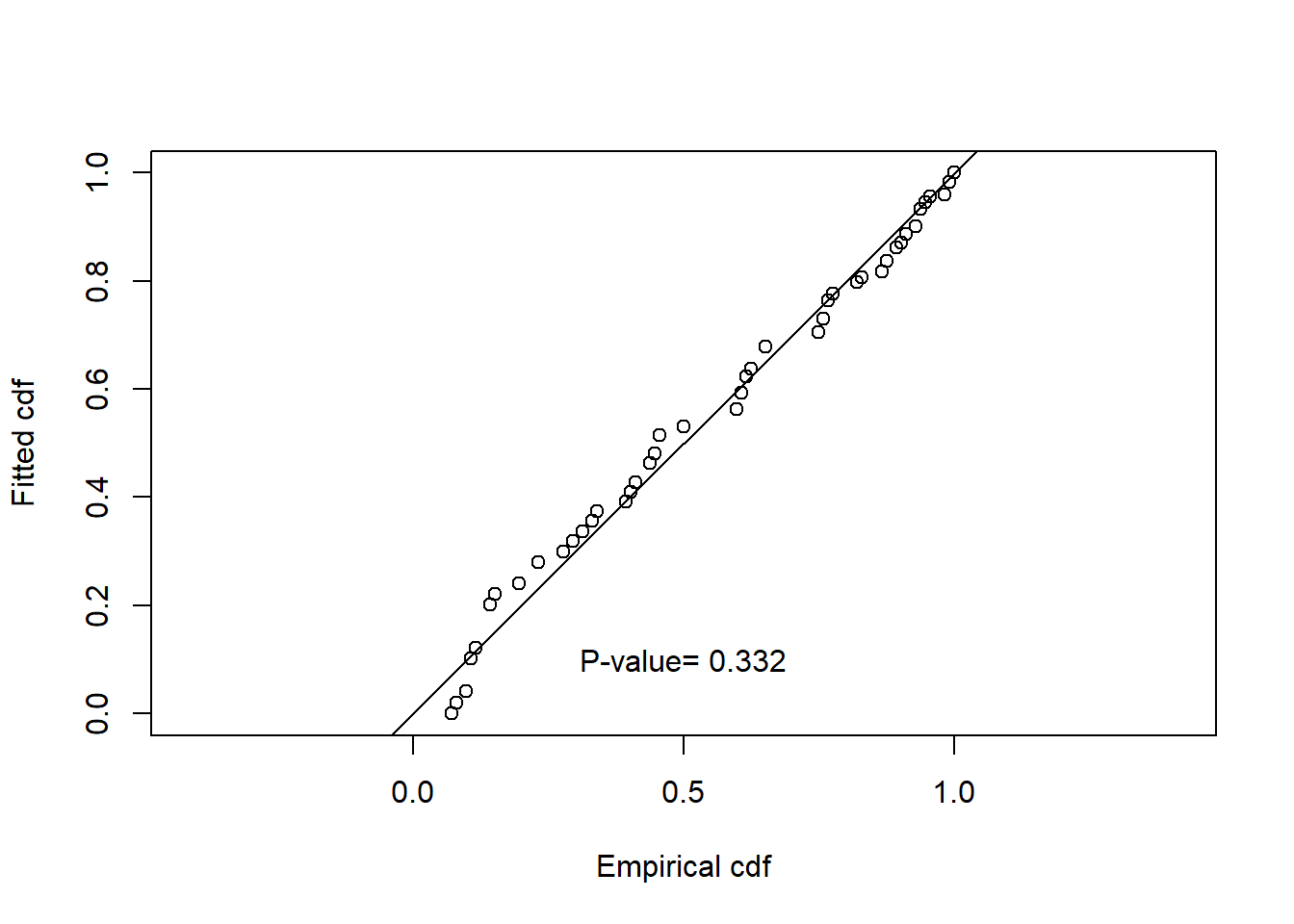
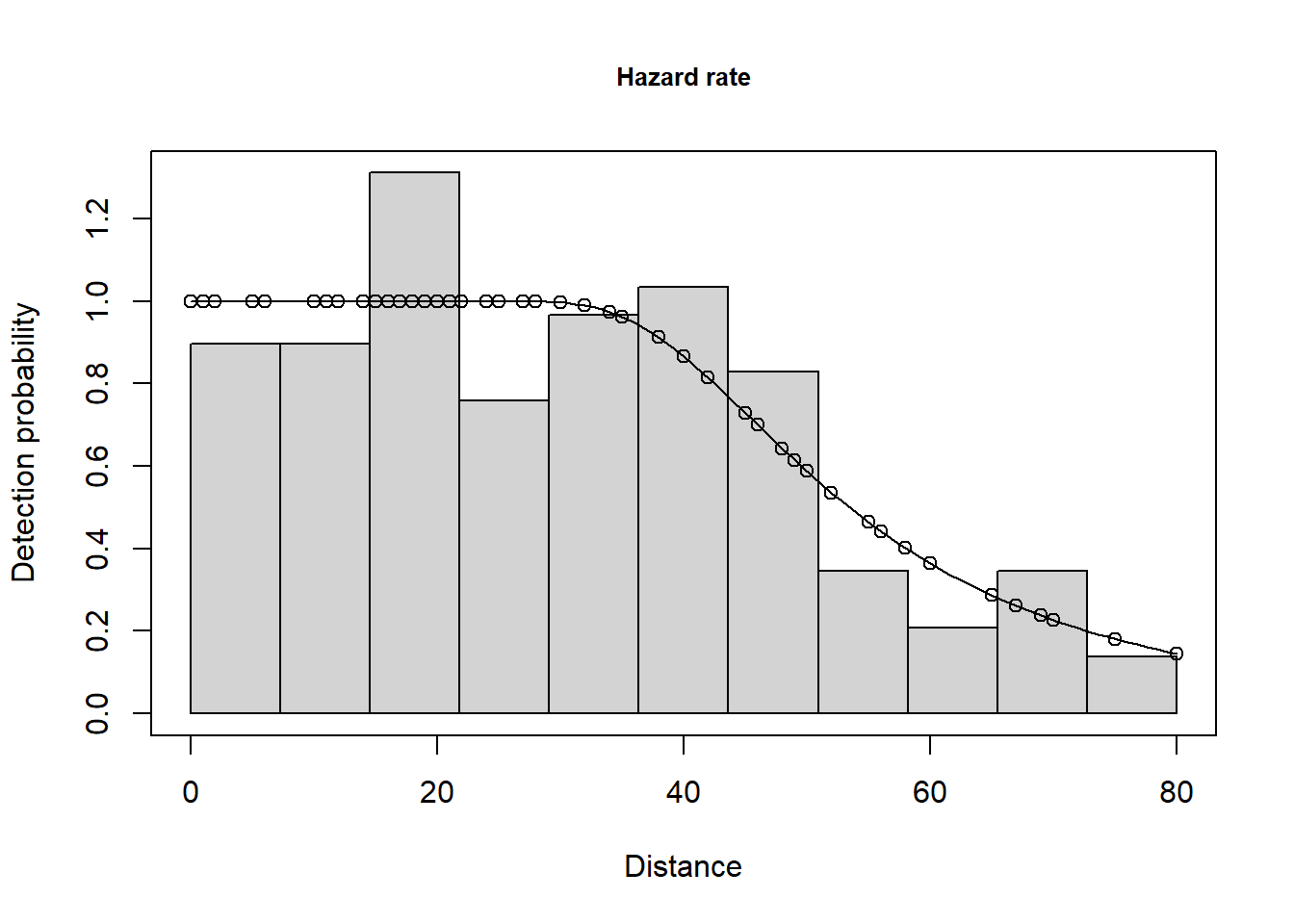
plot(caper.hr.cos, main="Hazard rate")
x <- gof_ds(caper.hr.cos)
text(.5, .1, paste("P-value=", round(x$dsgof$CvM$p,3)))
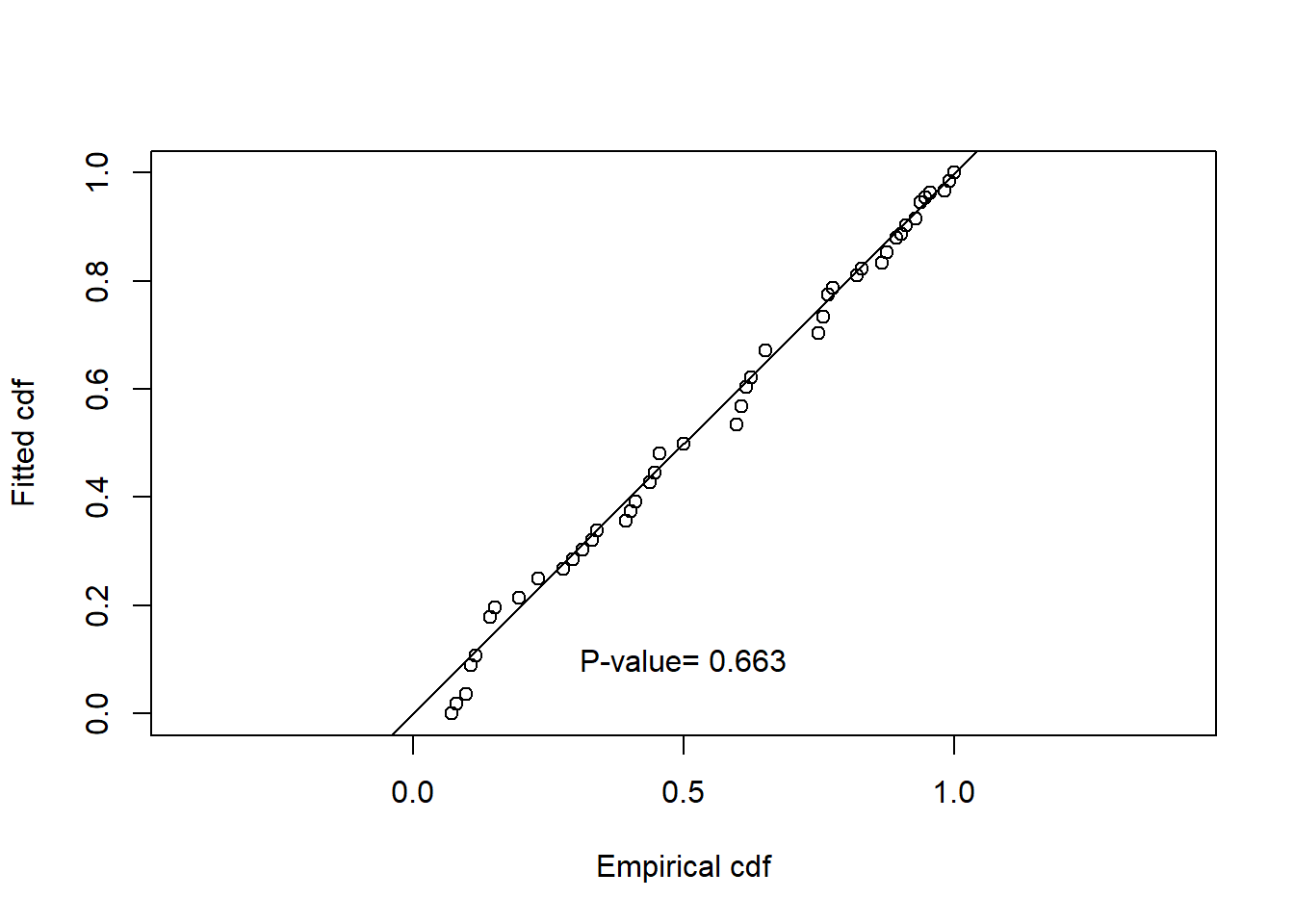
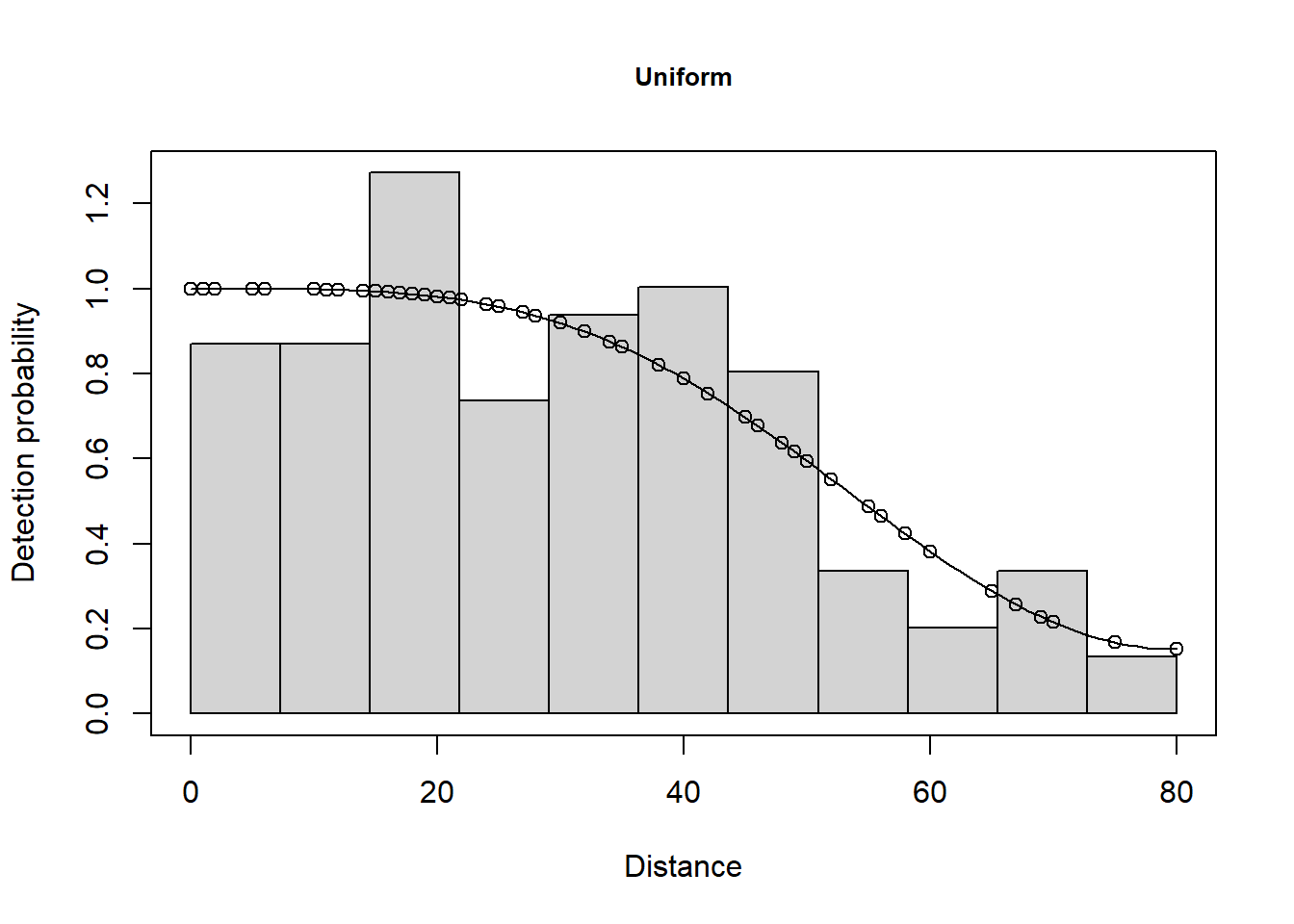
plot(caper.uf.cos, main="Uniform")
x <- gof_ds(caper.uf.cos)
text(.5, .1, paste("P-value=", round(x$dsgof$CvM$p,3)))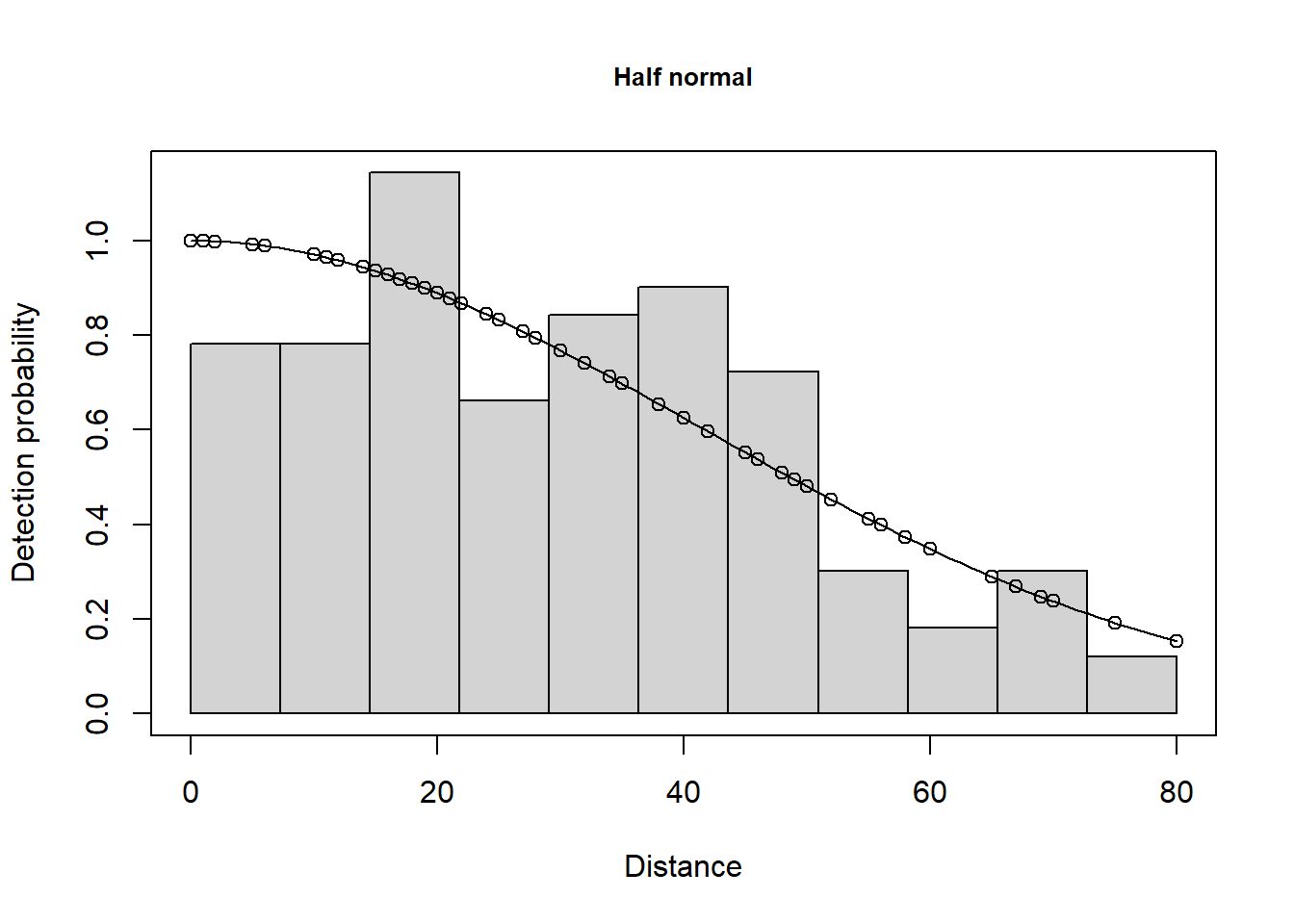

Half normal

QQ plot half normal

Hazard rate

QQ plot hazard rate

Uniform with adjustment

QQ plot uniform adj

Summarise the goodness of fit statistics (in a pretty format). This table indicates that the hazard rate detection function had the lowest AIC but the difference in AIC between all three models was small.

knitr::kable(summarize_ds_models(caper.hn.cos, caper.hr.cos, caper.uf.cos, output="plain"),
               caption="Summary of results of Capercaillie analysis.", digits = 3)
Summary of results of Capercaillie analysis.
Model Key function Formula C-vM \(p\)-value Average detectability se(Average detectability) Delta AIC
2 caper.hr.cos Hazard-rate ~1 0.663 0.703 0.052 0.000
1 caper.hn.cos Half-normal ~1 0.332 0.613 0.053 0.031
3 caper.uf.cos Uniform with cosine adjustment terms of order 1,2 NA 0.613 0.682 0.098 0.280

The results for the three different models are shown below: density is in birds per ha.

Capercaillie point estimates of density and associated measures of precision.
DetectionFunction AIC Pa Density D.CV Lower.CI Upper.CI
Half-normal 957.905 0.613 0.048 0.148 0.027 0.083
Hazard rate 957.874 0.703 0.042 0.148 0.020 0.084
Uniform 958.153 0.682 0.043 0.191 0.026 0.069

These capercaillie data are reasonably well-behaved and different models that fit the data well should give similar results.

Converting exact distances to binned distances

To deal with rounding in the distance data, the exact distances can be converted into binned distances. The cutpoints need to be chosen with care so that the distance bins are sufficiently wide enough to ensure that the ‘correct’ perpendicular distance is in the band containing the rounded recorded value. The bin widths do not have to be equal, as shown in example here: the cutpoints are 0, 7.5, 17.5, 27.5, …, 67.5, 80.0 m. Note, that any distances beyond the largest bin will be excluded.

# Specify (uneven) cutpoint for bins
bins <- c(0, seq(from=7.5, to=67.5, by=10), 80)
print(bins)
[1]  0.0  7.5 17.5 27.5 37.5 47.5 57.5 67.5 80.0
caper.hn.bin <- ds(data=capercaillie, key="hn", adjustment="cos", cutpoints=bins,
                   convert_units=conversion.factor)
plot(caper.hn.bin, main="Capercaillie, binned distances")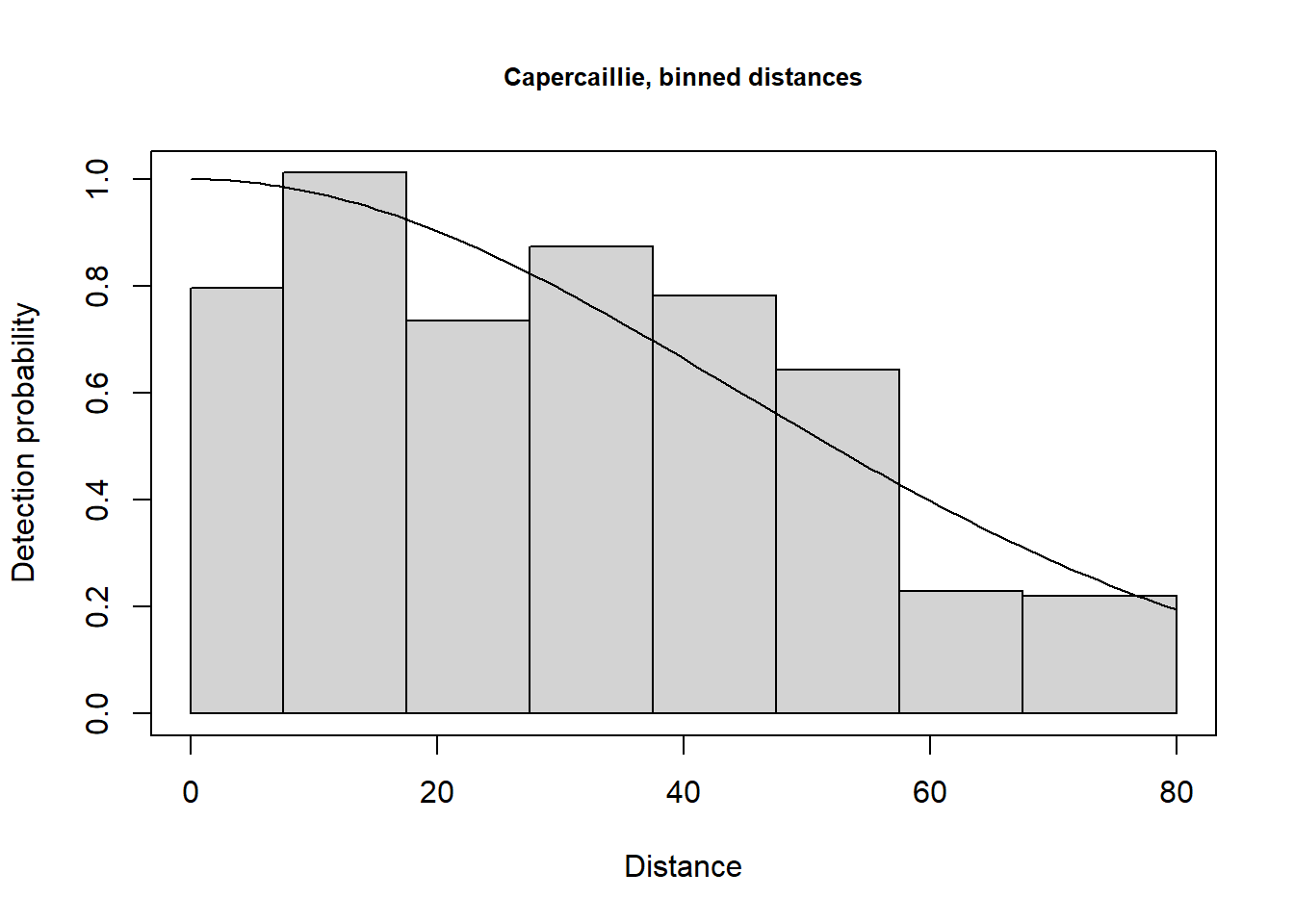

# See a portion of the results
knitr::kable(caper.hn.bin$dht$individuals$summary, row.names = FALSE)
Region Area CoveredArea Effort n k ER se.ER cv.ER mean.size se.mean
Monaughty Forest 1472 3840 240 112 1 0.4666667 0 0 1 0 
knitr::kable(caper.hn.bin$dht$individuals$D[1:6], row.names = FALSE, digits=3)
Label Estimate se cv lcl ucl
Total 0.045 0.007 0.152 0.026 0.079

Note that the binning of the data results in virtually identical estimates of density (0.045 birds per ha) and essentially no change in the precision of the density estimate compared with the estimates with analysis of exact distance data.