Analysis of data from stratified surveys solution

Author

Centre for Research into Ecological and Environmental Modelling
University of St Andrews

Modified

November 2024

Solution

Analysis of data from stratified surveys

Reading in the data from the stratified survey in the Southern Ocean:

library(Distance)
library(kableExtra)
# Load data
data(minke)
head(minke, n=3)
  Region.Label  Area Sample.Label Effort distance object
1        South 84734            1  86.75     0.10      1
2        South 84734            1  86.75     0.22      2
3        South 84734            1  86.75     0.16      3
# Specify truncation distance
minke.trunc <- 1.5

Strata treated distinctly

Fit detection function and encounter rate separately in each strata.

## Fit to each region separately - full geographical stratification
# Create data set for South
minke.S <- minke[minke$Region.Label=="South", ]
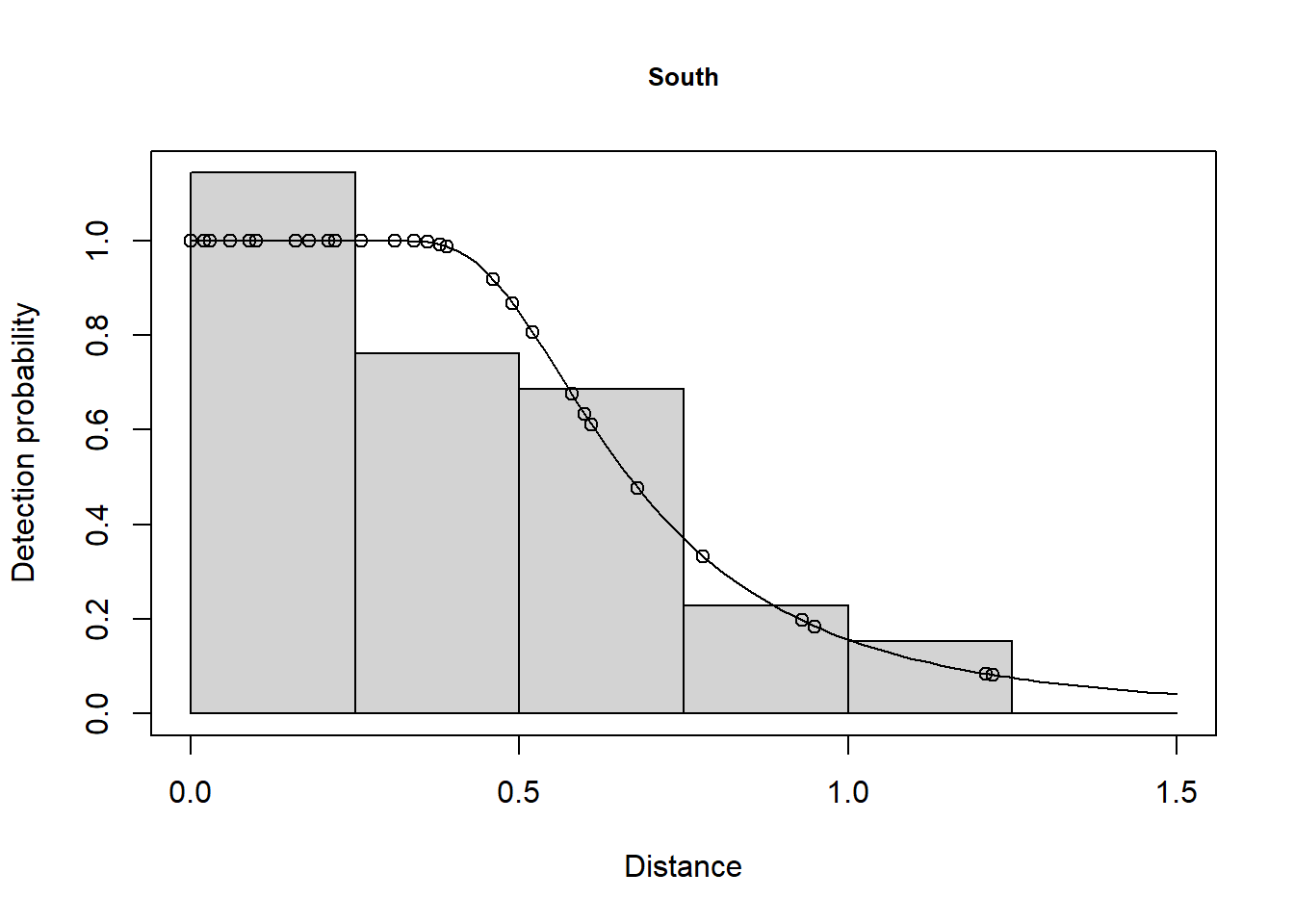
minke.df.S.strat <- ds(minke.S, truncation=minke.trunc, key="hr", adjustment=NULL)
summary(minke.df.S.strat)

Summary for distance analysis 
Number of observations :  39 
Distance range         :  0  -  1.5 

Model       : Hazard-rate key function 
AIC         :  8.617404 
Optimisation:  mrds (nlminb) 

Detection function parameters
Scale coefficient(s):  
              estimate        se
(Intercept) -0.5102606 0.1921723

Shape coefficient(s):  
            estimate        se
(Intercept) 1.242147 0.3770239

                      Estimate         SE       CV
Average p            0.4956459  0.0662961 0.133757
N in covered region 78.6852057 13.8143714 0.175565

Summary statistics:
  Region  Area CoveredArea Effort  n  k         ER      se.ER     cv.ER
1  South 84734     1453.23 484.41 39 13 0.08051031 0.01809954 0.2248102

Abundance:
  Label Estimate       se        cv      lcl      ucl       df
1 Total 4587.926 1200.166 0.2615924 2687.497 7832.219 21.14052

Density:
  Label   Estimate         se        cv        lcl        ucl       df
1 Total 0.05414505 0.01416393 0.2615924 0.03171687 0.09243301 21.14052
# Combine selection and detection function fitting for North
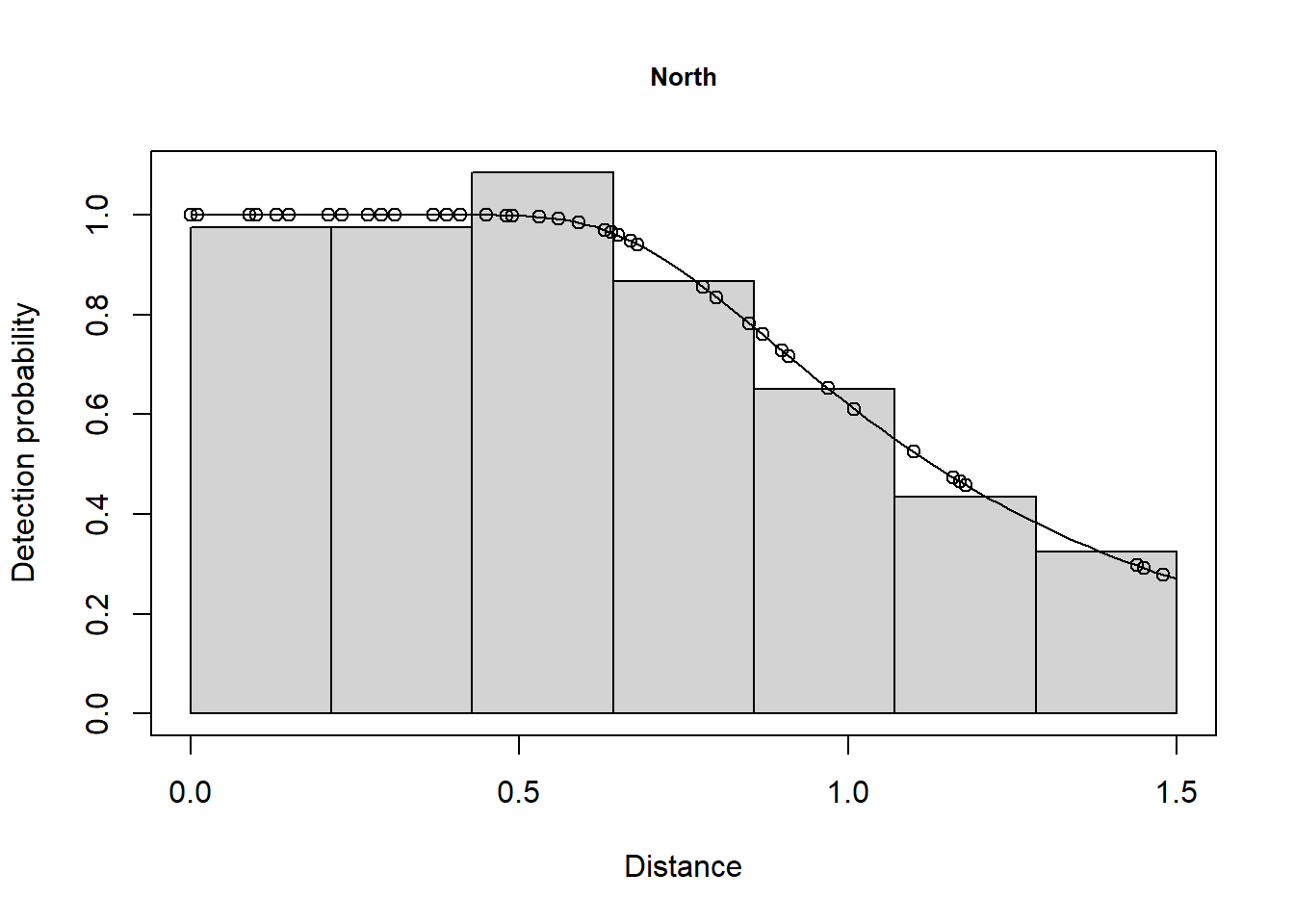
minke.df.N.strat <- ds(minke[minke$Region.Label=="North", ],
                       truncation=minke.trunc, key="hr", adjustment=NULL)
summary(minke.df.N.strat)

Summary for distance analysis 
Number of observations :  49 
Distance range         :  0  -  1.5 

Model       : Hazard-rate key function 
AIC         :  37.27825 
Optimisation:  mrds (nlminb) 

Detection function parameters
Scale coefficient(s):  
               estimate        se
(Intercept) -0.01081049 0.2203527

Shape coefficient(s):  
            estimate        se
(Intercept) 1.022021 0.6907908

                      Estimate         SE        CV
Average p            0.7592309 0.09987677 0.1315499
N in covered region 64.5389996 9.62021709 0.1490605

Summary statistics:
  Region   Area CoveredArea  Effort  n  k         ER      se.ER     cv.ER
1  North 630582     4075.14 1358.38 49 12 0.03607238 0.01317937 0.3653591

Abundance:
  Label Estimate       se        cv      lcl     ucl       df
1 Total 9986.683 3878.032 0.3883203 4469.865 22312.5 13.98197

Density:
  Label   Estimate          se        cv         lcl        ucl       df
1 Total 0.01583725 0.006149924 0.3883203 0.007088475 0.03538397 13.98197

Detections combined across strata

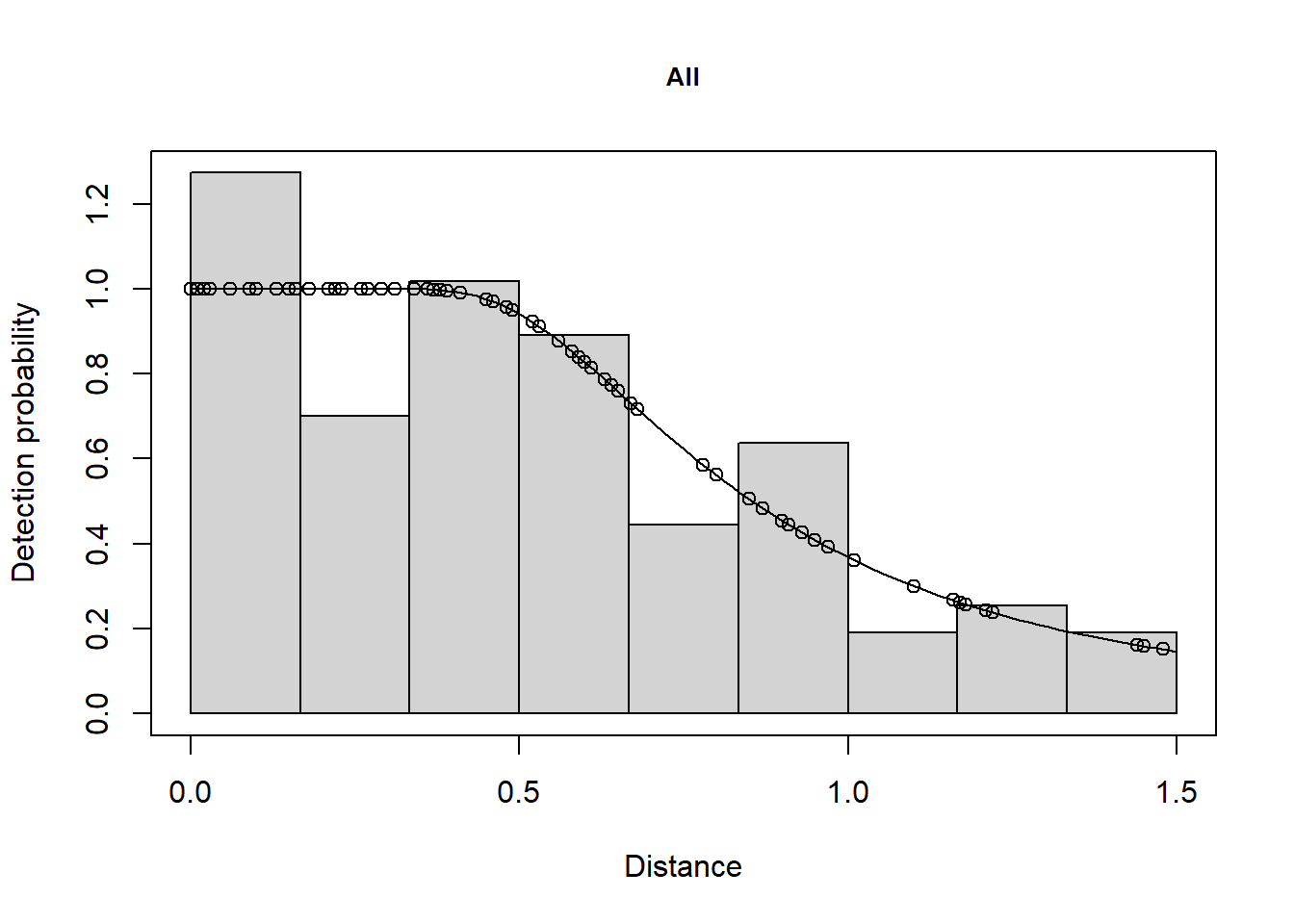
Next we fitted a pooled detection function.

minke.df.all <- ds(minke, truncation=minke.trunc, key="hr", adjustment=NULL)
summary(minke.df.all)

Summary for distance analysis 
Number of observations :  88 
Distance range         :  0  -  1.5 

Model       : Hazard-rate key function 
AIC         :  48.63688 
Optimisation:  mrds (nlminb) 

Detection function parameters
Scale coefficient(s):  
              estimate        se
(Intercept) -0.2967912 0.1765812

Shape coefficient(s):  
             estimate        se
(Intercept) 0.9648331 0.3605009

                       Estimate         SE        CV
Average p             0.6224396  0.0668011 0.1073214
N in covered region 141.3791718 17.7757784 0.1257312

Summary statistics:
  Region   Area CoveredArea  Effort  n  k         ER      se.ER     cv.ER
1  North 630582     4075.14 1358.38 49 12 0.03607238 0.01317937 0.3653591
2  South  84734     1453.23  484.41 39 13 0.08051031 0.01809954 0.2248102
3  Total 715316     5528.37 1842.79 88 25 0.04133635 0.01181436 0.2858103

Abundance:
  Label  Estimate        se        cv      lcl       ucl       df
1 North 12181.419 4638.6283 0.3807954 5499.950 26979.692 12.96781
2 South  3653.345  910.0975 0.2491135 2181.595  6117.971 17.96263
3 Total 15834.764 4834.2848 0.3052957 8388.423 29891.167 15.25496

Density:
  Label   Estimate          se        cv         lcl        ucl       df
1 North 0.01931774 0.007356106 0.3807954 0.008722023 0.04278538 12.96781
2 South 0.04311546 0.010740641 0.2491135 0.025746391 0.07220207 17.96263
3 Total 0.02213674 0.006758251 0.3052957 0.011726878 0.04178736 15.25496

Compute combined AIC for entire study area.

aic.all <- summary(minke.df.all$ddf)$aic
aic.S <- summary(minke.df.S.strat$ddf)$aic
aic.N <- summary(minke.df.N.strat$ddf)$aic
aic.SN <- aic.S + aic.N

Determining the correct stratification to use

The AIC value for the detection function in the South was 8.617 and the AIC for the North was 37.28. This gives a total AIC of 45.9. The AIC value for the pooled detection function was 48.64. Because 48.64 is greater than 45.9, estimation of separate detection functions in each stratum is preferable.

Differing abundance estimates from stratification decision

In the full geographical stratification, both encounter rate and detection function were estimated separately for each region (or strata). This resulted in the following abundances:

Abundance estimates using full geographical stratification.
Label Estimate
North 9987
South 4588
Total 14575

Next, the distances were combined to fit a pooled detection function but encounter rate was obtained for each region. This resulted in the following abundances:

Abundance estimates calculating encounter rate by strata and a pooled detection function.
Label Estimate
North 12181
South 3653
Total 15835

Another approach to stratification (advanced)

An equivalent result for full geographic stratification could be produced using the dht2 function, which does not require the disaggregation of the data set into two data sets.

# Geographical stratification with stratum-specific detection function 
strat.specific.detfn <- ds(data=minke, truncation=minke.trunc, key="hr", 
                           adjustment=NULL, formula=~Region.Label)
abund.by.strata <- dht2(ddf=strat.specific.detfn, flatfile=minke, 
                        strat_formula=~Region.Label, stratification="geographical")
print(abund.by.strata, report="abundance")
Abundance estimates from distance sampling
Stratification : geographical 
Variance       : R2, n/L 
Multipliers    : none 
Sample fraction : 1 


Summary statistics:
 Region.Label   Area CoveredArea  Effort  n  k    ER se.ER cv.ER
        North 630582     4075.14 1358.38 49 12 0.036 0.013 0.365
        South  84734     1453.23  484.41 39 13 0.081 0.018 0.225
        Total 715316     5528.37 1842.79 88 25 0.048 0.011 0.237

Abundance estimates:
 Region.Label Estimate       se    cv  LCI   UCI     df
        North     9865 3761.296 0.381 4451 21860 13.035
        South     4651 1224.818 0.263 2719  7955 22.163
        Total    14515 3970.578 0.274 8215 25648 16.065

Component percentages of variance:
 Region.Label Detection    ER
        North      8.18 91.82
        South     27.13 72.87
        Total     12.49 87.51

I won’t say anything just now about the wrinkle I introduced with the formula argument in the call to ds(). Recognise there is an alternative (easier) way to perform the full geographic stratification analysis without tearing apart the data. The abundance estimates presented in the last output do not identically match the estimates shown earlier for full geographic stratification, but they are close. The added benefit of this latter analysis is that the uncertainty in the total population size is computed within dht2 rather than needing to be calculated manually using the delta method.

An aside

If geographic stratification were ignored, the abundance estimate of would be 18,293 minkes. This estimate is substantially larger than the estimates above. The reason is that the survey design was geographically stratified with a smaller proportion of the north stratum receiving sampling effort and a greater proportion of the southern stratum receiving survey effort. Ignoring this inequity in the unstratified analysis would lead us to believe that the more heavily sampled southern stratum is indicative of whale density throughout the study area.