Analysis of double-platform data

Analysis of double-platform data

This version of the practical is for those who would like to conduct the analysis in R using the package mrds (Laake et al., 2024). There is a separate version for conducting the analysis in Distance for Windows (Thomas et al., 2010).

The first part of this practical involves initial analysis of a survey of a known number of golf tees. This is intended mainly to familiarise you with the mrds function.

The second part of the practical involves more detailed analysis of the golf tee data, and an exploration of the double-platform data structure.

The third part of the practical involves analysis of the pack-ice seal survey data of Borchers et al. (2006) and Southwell et al. (2007).

To help understand the terminology used in MRDS and the output produced by mrds, there is a guide available ‘Interpreting MRDS output’.

Golf tee survey - initial analysis

Golf tee survey

These data come from a survey of golf tees which conducted by statistics students at the University of St Andrews. The data were collected along transect lines, 210 metres in total. A distance of 4 metres out from the centre line was searched and, for the purposes of this exercise, we assume that this comprised the total study area, which was divided into two strata. There were 250 clusters of tees in total and 760 individual tees in total.

The population was independently surveyed by two observer teams. The following data were recorded for each detected group: perpendicular distance, cluster size, observer (team 1 or 2), ‘sex’ (males are yellow and females are green and golf tees occur in single-sex clusters) and ‘exposure’. Exposure was a subjective judgment of whether the cluster was substantially obscured by grass (exposure=0) or not (exposure=1). The lengths of grass varied along the transect line and the grass was slightly more yellow along one part of the line compared to the rest.

The golf tee dataset is provided as part of the mrds package.

Open R and load the mrds package and golf tee dataset (called book.tee.data). The elements required for an MRDS analysis are contained within the object dataset. These data are in a hierarchical structure (rather than in a ‘flat file’ format) so that there are separate elements for observations, samples and regions. In the code below, each of these tables is extracted to avoid typing long names.

# Load libraries
library(knitr) #Used to knit this markdown document together
library(mrds)
#Note - the Distance package is also used in the Crabeater seal example, to access
# the checkdata function, and to do an MCDS analysis.

# Access the golf tee data
data(book.tee.data)

# Extract the list elements from the dataset into easy-to-access objects
detections <- book.tee.data$book.tee.dataframe # detection information
region <- book.tee.data$book.tee.region # region info
samples <- book.tee.data$book.tee.samples # transect info
obs <- book.tee.data$book.tee.obs # links detections to transects and regions

# In the detections data frame, define sex and exposure as factor variables 
detections$sex <- as.factor(detections$sex)
detections$exposure <- as.factor(detections$exposure)

Golf tee survey analyses

Estimation of p: distance only

We will start by analysing these data assuming that Observer 2 was generating trials for Observer 1 but not vice versa, i.e. trial configuration where Observer 1 is the primary and Observer 2 is the tracker. (The data could also be analysed in independent observer configuration - you are welcome to try this for yourself). We begin by assuming full independence (i.e. detections between observers are independent at all distances): this requires only a mark-recapture (MR) model and, to start with, perpendicular distance will be included as the only covariate.

Remember that ? or help can be used to find out more about any of the functions used – e.g., ?ddf will tell you more about the ddf function.

# Fit trial configuration with full independence model
fi.mr.dist <- ddf(method='trial.fi', mrmodel=~glm(link='logit',formula=~distance),
                  data=detections, meta.data=list(width=4))

Examining mrds output

Having fitted the model, we can create tables summarizing the detection data. In the commands below, the tables are created using the det.tables function and saved to detection.tables.

# Create a set of tables summarizing the double observer data 
detection.tables <- det.tables(fi.mr.dist)
# Print these detection tables
detection.tables

Observer 1 detections
           Detected
            Missed Detected
  [0,0.4]        1       25
  (0.4,0.8]      2       16
  (0.8,1.2]      2       16
  (1.2,1.6]      6       22
  (1.6,2]        5        9
  (2,2.4]        2       10
  (2.4,2.8]      6       12
  (2.8,3.2]      6        9
  (3.2,3.6]      2        3
  (3.6,4]        6        2

Observer 2 detections
           Detected
            Missed Detected
  [0,0.4]        4       22
  (0.4,0.8]      1       17
  (0.8,1.2]      0       18
  (1.2,1.6]      2       26
  (1.6,2]        1       13
  (2,2.4]        2       10
  (2.4,2.8]      3       15
  (2.8,3.2]      4       11
  (3.2,3.6]      2        3
  (3.6,4]        1        7

Duplicate detections

  [0,0.4] (0.4,0.8] (0.8,1.2] (1.2,1.6]   (1.6,2]   (2,2.4] (2.4,2.8] (2.8,3.2] 
       21        15        16        20         8         8         9         5 
(3.2,3.6]   (3.6,4] 
        1         1 

Observer 1 detections of those seen by Observer 2
          Missed Detected Prop. detected
[0,0.4]        1       21      0.9545455
(0.4,0.8]      2       15      0.8823529
(0.8,1.2]      2       16      0.8888889
(1.2,1.6]      6       20      0.7692308
(1.6,2]        5        8      0.6153846
(2,2.4]        2        8      0.8000000
(2.4,2.8]      6        9      0.6000000
(2.8,3.2]      6        5      0.4545455
(3.2,3.6]      2        1      0.3333333
(3.6,4]        6        1      0.1428571

The information in detection summary tables can be plotted, but, in the interest of space, only one (out of six possible plots) is shown below.

# Plot detection information, change number to see other plots
plot(detection.tables, which=1)

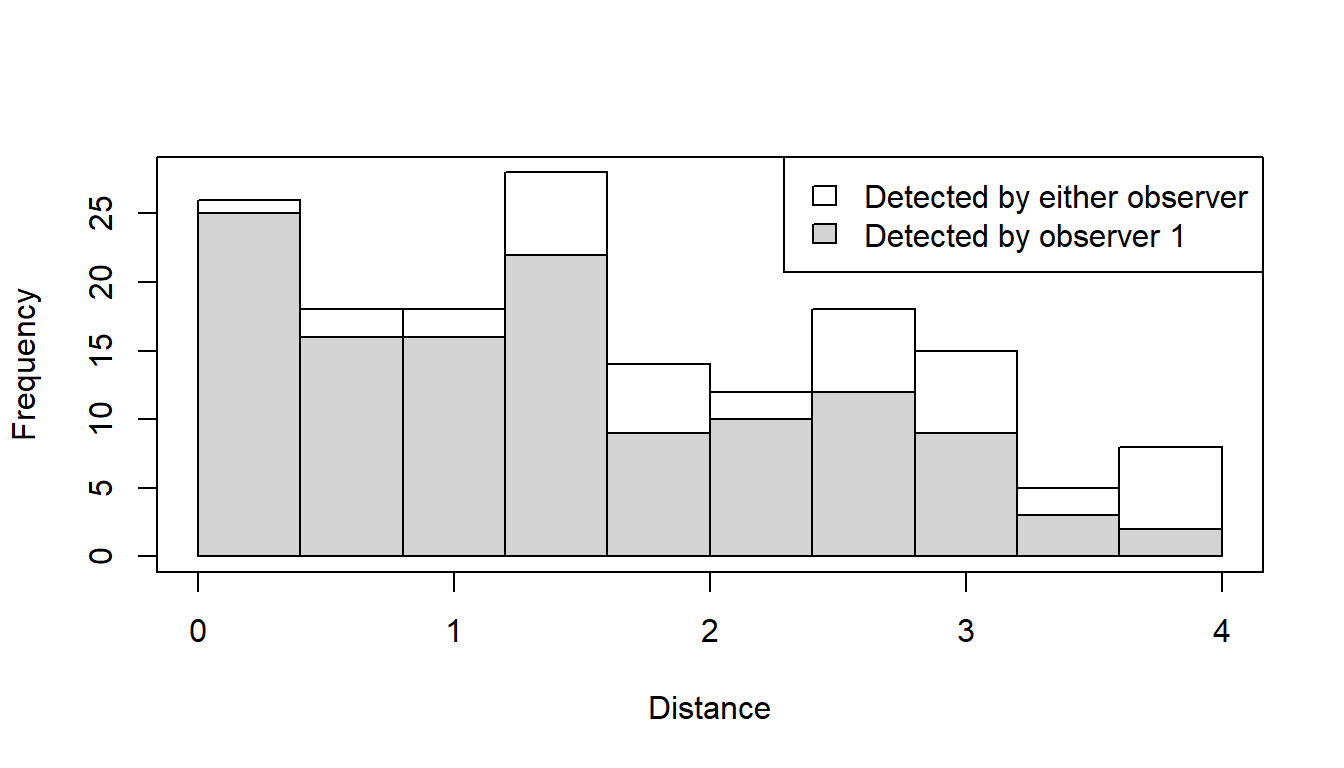
The plot numbers are:

1. Histograms of distances for detections by either, or both, observers. The shaded regions show the number for observer 1.
2. Histograms of distances for detections by either, or both, observers. The shaded regions show the number for observer 2.
3. Histograms of distances for duplicates (detected by both observers).
4. Histogram of distances for detections by either, or both, observers. Not shown for trial configuration.
5. Histograms of distances for observer 2. The shaded regions indicate the number of duplicates - for example, the shaded region is the number of clusters in each distance bin that were detected by Observer 1 given that they were also detected by Observer 2 (the “|” symbol in the plot legend means “given that”).
6. Histograms of distances for observer 1. The shaded regions indicate the number of duplicates as for plot 5. Not shown for trial configuration.

Note that if an independent observer configuration had been chosen, all plots would be available.

A summary of the detection function model is available using the summary function. The Q-Q plot has the same interpretation as a Q-Q plot in a conventional, single platform analysis.

# Produce a summary of the fitted detection function object
summary(fi.mr.dist)

Summary for trial.fi object 
Number of observations               :  162 
Number seen by primary               :  124 
Number seen by secondary (trials)    :  142 
Number seen by both (detected trials):  104 
AIC                                  :  452.8094 


Conditional detection function parameters:
             estimate        se
(Intercept)  2.900233 0.4876238
distance    -1.058677 0.2235722

                        Estimate          SE         CV
Average p              0.6423252  0.04069410 0.06335435
Average primary p(0)   0.9478579  0.06109656 0.06445750
N in covered region  193.0486185 15.84826582 0.08209469

# Produce goodness of fit statistics and a qq plot
gof.result <- ddf.gof(fi.mr.dist, 
                      main="Full independence, trial configuration\ngoodness of fit Golf tee data")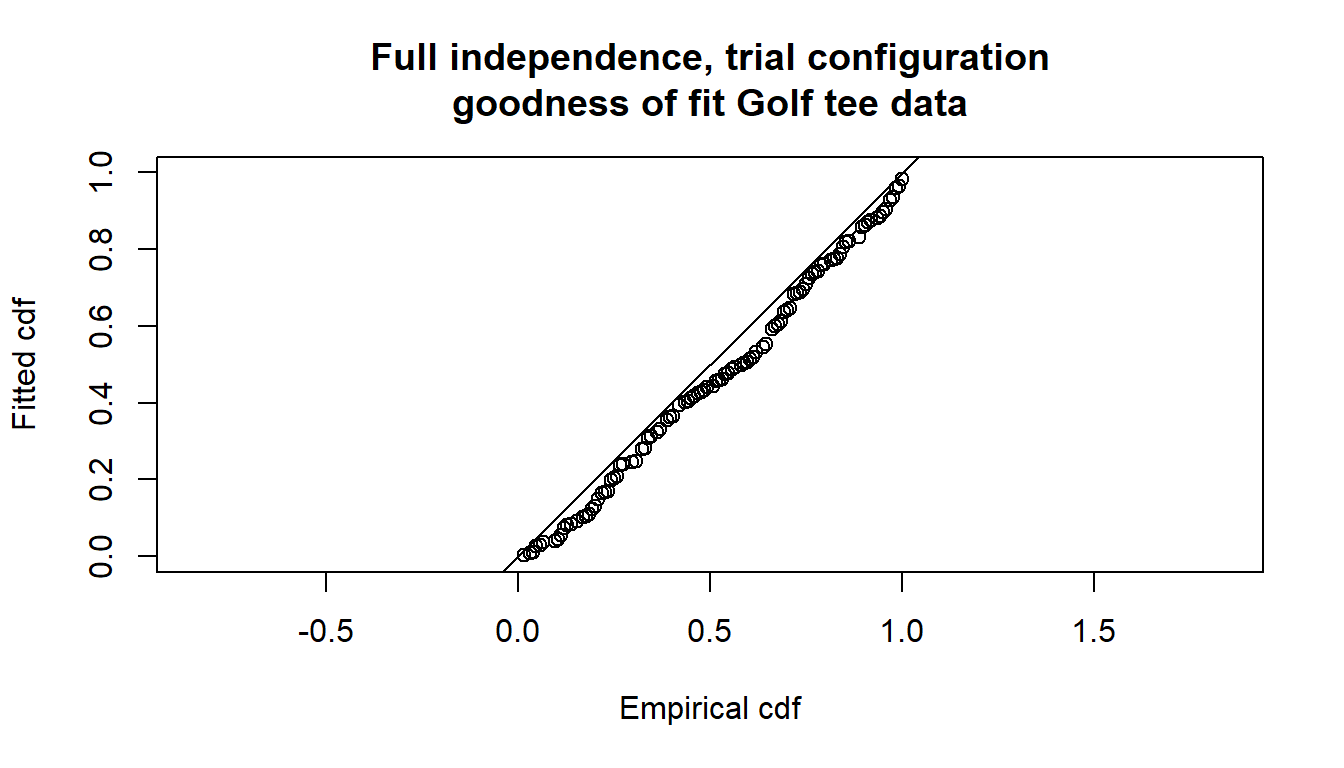

gof.result

Goodness of fit results for ddf object

Chi-square tests

Distance sampling component:
          [0,0.4] (0.4,0.8] (0.8,1.2] (1.2,1.6] (1.6,2] (2,2.4] (2.4,2.8]
Observed   25.000    16.000    16.000    22.000   9.000  10.000    12.000
Expected   18.068    17.479    16.650    15.527  14.079  12.327    10.361
Chisquare   2.659     0.125     0.025     2.698   1.833   0.439     0.259
          (2.8,3.2] (3.2,3.6] (3.6,4]   Total
Observed      9.000     3.000   2.000 124.000
Expected      8.335     6.419   4.753 124.000
Chisquare     0.053     1.821   1.595  11.508

No degrees of freedom for test

Mark-recapture component:
Capture History 01
          [0,0.4] (0.4,0.8] (0.8,1.2] (1.2,1.6] (1.6,2] (2,2.4] (2.4,2.8]
Observed        1         2         2         6       5       2         6
Expected        1         2         3         5       4       4         7
Chisquare       0         0         0         0       1       1         0
          (2.8,3.2] (3.2,3.6] (3.6,4] Total
Observed          6         2       6    38
Expected          6         2       5    38
Chisquare         0         0       0     2
Capture History 11
          [0,0.4] (0.4,0.8] (0.8,1.2] (1.2,1.6] (1.6,2] (2,2.4] (2.4,2.8]
Observed       21        15        16        20       8       8         9
Expected       21        15        15        21       9       6         8
Chisquare       0         0         0         0       0       0         0
          (2.8,3.2] (3.2,3.6] (3.6,4] Total
Observed          5         1       1   104
Expected          5         1       2   104
Chisquare         0         0       0     1


Total chi-square = 14.888  P = 0.60351 with 17 degrees of freedom

Distance sampling Cramer-von Mises test (unweighted)
Test statistic = 0.294564 p-value = 0.140034

# Extract chi-square statistics for reporting in the text below (see Markdown file for how this is done).
chi.distance <- gof.result$chisquare$chi1$chisq
chi.markrecap <- gof.result$chisquare$chi2$chisq
chi.total <- gof.result$chisquare$pooled.chi

The \(\chi^2\) goodness-of-fit assessment shows the \(\chi^2\) contribution from the distance sampling component to be 11.5 and the \(\chi^2\) contribution from the mark-recapture component to be 3.4. The combination of these elements produces a total \(\chi^2\) of 14.9 with 17 degrees of freedom, resulting in a \(p\)-value of 0.604

The mark-recapture model detection function can be plotted with the following code:

# Divide the plot region into 2 columns
par(mfrow=c(1,2))
# Plot detection functions
plot(fi.mr.dist)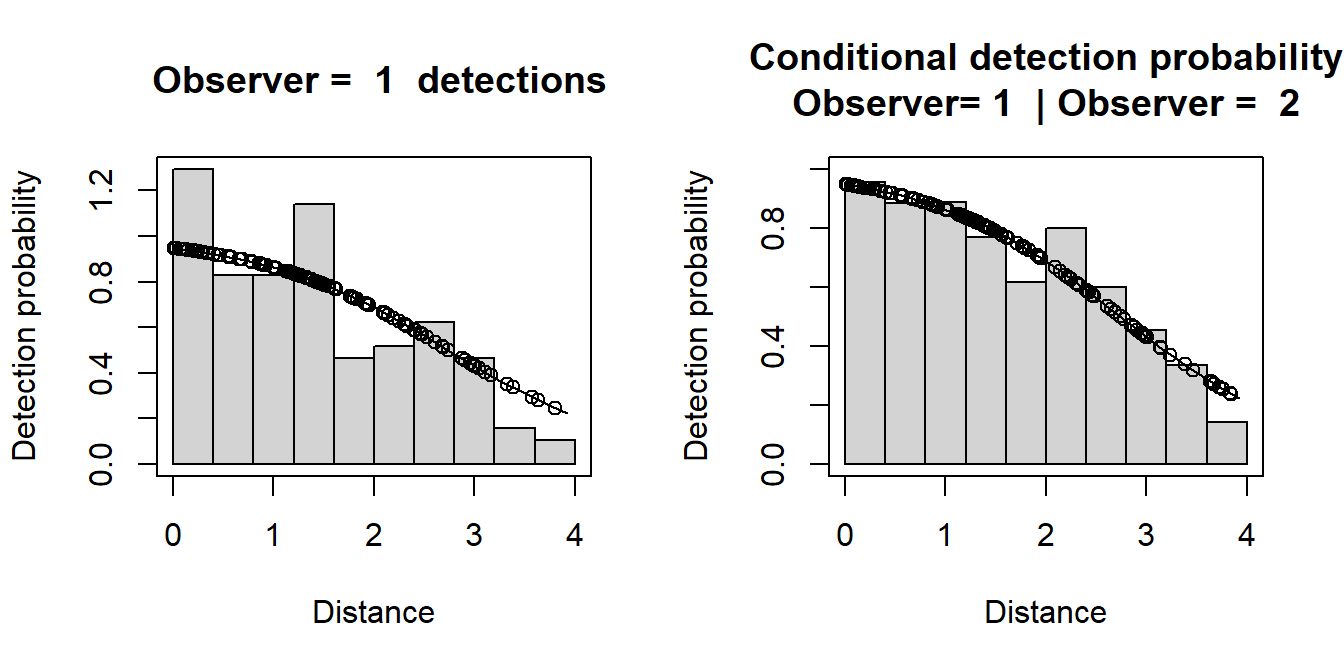

The plot headed

• “Conditional detection probability” (the right hand plot) shows the proportion of Obs 2’s detections that were detected by Obs 1 (also see the detection tables). The fitted line is the estimated detection probability function for Obs 1 (given detection by Obs 2) - this is the MR model. Dots are estimated detection probabilities for each Obs 1 detection.
• “Observer=1 detections” (left hand plot) shows a histogram of Observer 1 detections with the estimated Observer 1 detection function (from the MR model) overlaid on it and adjusted for the estimated p(0). The dots show the estimated detection probability for all Observer 1 detections. Note that the MR model was not fitted to these data – it is the conditional data (right hand plot) that was used to fit the model. This plot is just shown to help you diagnose any issues in the fit – if there is dependency between observer detections then we’d expect the detection function to decrease slower than the histograms.

Is there evidence of unmodelled heterogeneity? What do these results tell you about the estimates of p (average detection probability) and p(0) (detection probability at 0 distance)?

Estimating abundance

Abundance is estimated using the dht function. In this function, we need to supply information about the transects and survey regions.

# Calculate density estimates using the dht function
tee.abund <- dht(model=fi.mr.dist, region.table=region, sample.table=samples, 
                 obs.table=obs)

# Print out results in a nice format
knitr::kable(tee.abund$individuals$summary, digits=2, 
      caption="Survey summary statistics for golftees")

Survey summary statistics for golftees

Region	Area	CoveredArea	Effort	n	k	ER	se.ER	cv.ER	mean.size	se.mean
1	1040	1040	130	229	6	1.76	0.12	0.07	3.18	0.21
2	640	640	80	152	5	1.90	0.33	0.18	2.92	0.23
Total	1680	1680	210	381	11	1.81	0.15	0.08	3.07	0.15

knitr::kable(tee.abund$individuals$N, digits=2, 
      caption="Abundance estimates for golftee population with two strata")

Abundance estimates for golftee population with two strata

Label	Estimate	se	cv	lcl	ucl	df
1	356.52	32.35	0.09	294.54	431.53	17.13
2	236.64	44.14	0.19	147.33	380.09	5.06
Total	593.16	60.38	0.10	478.32	735.57	16.06

Estimation of p: distance and other explanatory variables

Below is a model that includes size, sex and exposure covariates. Please spend a bit of time examining the model coefficients, goodness of fit, plots of the fitted detection functions, etc (you’ll need to write your own code for this).

# Example of adding covariates to MR detection function
fi.mr.dist.size.sex.exposure <- ddf(method='trial.fi', 
                      mrmodel=~glm(link='logit',formula=~distance+size+sex+exposure),
                      data=detections, meta.data=list(width=4))

We can use AIC to compare this with the previous model that just had distance as a covariate. The function AIC works on these objects:

AIC(fi.mr.dist, fi.mr.dist.size.sex.exposure)

                             df      AIC
fi.mr.dist                    2 452.8094
fi.mr.dist.size.sex.exposure  5 407.3974

Golf tee survey

Further analyses of golf tee data

Estimation of p: distance and other explanatory variables

The size covariate is the least significant of the covariates in the model fi.mr.dist.size.sex.exposure – its estimate is 0.078 with SE 0.183. So try creating a new model definition and analysis without this covariate. Does it have a lower AIC?

You can also try some models with interaction terms - you can specify these in the usual way in the model foruma with a * symbol. Don’t spend too long on full independence models, but move on to the next section.

Point independence

A less restrictive assumption than full independence is point independence, which assumes that detections are only independent on the transect centre line i.e. at perpendicular distance zero.

Let’s start by seeing if a simple point independence model is better than a simple full independence one. This requires that a distance sampling (DS) model is specified as well a MR model. Here we try a half-normal key function for the DS model.

# Fit trial configuration with point independence model
pi.mr.dist <- ddf(method='trial', 
                  mrmodel=~glm(link='logit', formula=~distance),
                  dsmodel=~cds(key='hn'), 
                  data=detections, meta.data=list(width=4))

# Summary pf the model 
summary(pi.mr.dist)

Summary for trial.fi object 
Number of observations               :  162 
Number seen by primary               :  124 
Number seen by secondary (trials)    :  142 
Number seen by both (detected trials):  104 
AIC                                  :  140.8887 


Conditional detection function parameters:
             estimate        se
(Intercept)  2.900233 0.4876238
distance    -1.058677 0.2235722

                      Estimate         SE         CV
Average primary p(0) 0.9478579 0.02409996 0.02542571



Summary for ds object
Number of observations :  124 
Distance range         :  0  -  4 
AIC                    :  311.1385 
Optimisation           :  mrds (nlminb) 

Detection function:
 Half-normal key function 

Detection function parameters 
Scale coefficient(s): 
             estimate         se
(Intercept) 0.6632435 0.09981249

           Estimate         SE         CV
Average p 0.5842744 0.04637627 0.07937412


Summary for trial object

Total AIC value =  452.0272 
                       Estimate          SE         CV
Average p             0.5538091  0.04615832 0.08334697
N in covered region 223.9038534 22.99246338 0.10268900

# Produce goodness of fit statistics and a qq plot
gof.results <- ddf.gof(pi.mr.dist, main="Point independence, trial configuration\n goodness of fit Golftee data")

Compare the results with the corresponding full independence model. Which has the lower AIC? Which has an estimate closer to known true abundance.

Covariates in the DS model

To include covariates in the DS detection function, we need to specify an MCDS model as follows:

# Fit the PI-trial model - DS sex and MR distance 
pi.mr.dist.ds.sex <- ddf(method='trial', 
                         mrmodel=~glm(link='logit',formula=~distance),
                         dsmodel=~mcds(key='hn',formula=~sex), 
                         data=detections, meta.data=list(width=4))

Use the summary or AIC function to check the AIC and decide if you are going to include any additional covariates in the detection function.

Now try a point independence model that has the preferred MR model from your full independence analyses. Which has the lower AIC and bias?

Feel free to experiment some more with different models. What is your final best model? What is the estimate of p and p(0) for this model? Was all this modelling necessary in this instance, given the value of p(0)? How else could you have obtained a robust estimate of abundance?

Data structure

Before moving on to the second dataset, let’s have a look at the columns in the detections data because, for all mrds analyses, it needs to have a particular structure.

# Check detections
head(detections)

   object observer detected distance size sex exposure
1       1        1        1     2.68    2   1        1
21      1        2        0     2.68    2   1        1
2       2        1        1     3.33    2   1        0
22      2        2        0     3.33    2   1        0
3       3        1        1     0.34    1   0        0
23      3        2        0     0.34    1   0        0

The structure of the detection is as follows:

• each detected object (in this case the object was a group or cluster of golf tees) is given a unique number in the object column,
• each object occurs twice - once for observer 1 and once for observer 2,
• the detected column indicates whether the object was seen (detected=1) or not seen (detected=0) by the observer,
• perpendicular distance is in the distance column and cluster size is in the size column (the same default names as for the ds function).

To ensure that the variables sex and exposure are treated correctly, we defined them as factor variables.

Crabeater seal survey

Crabeater seal data

This analysis is described in Borchers et al. (2006) and Southwell et al. (2007). These data come from a helicopter survey of crabeater seals conducted by the Australian Antarctic Division within the pack-ice seals programme. The helicopter could only operate within a relatively short distance from the ice-breaker ship which acted as its base. The ice-breaker could only go where the pack ice was thin enough and so the aerial transects could not be located at random. This means that design-based estimation was not a valid option and so, in the published analysis, abundance was estimated using density surface modelling. For the purposes of this exercise, we concentrate on detection function estimation and create an artificial region as a device to produce abundance estimates.

There were four independent observers in the helicopter, two on each side (front and back). The front observers were considered to be one ‘team’ and the back observers were considered to be the other ‘team’. Various environmental factors were recorded. In addition to perpendicular distance, observer (1=front or 2=back) and cluster size, the following explanatory variables are available:

• side – the side of the helicopter from which seal were seen (L and R)
• exp – the experience (in survey hours) of the observer
• fatigue – the number of minutes the observer had been on duty on the current flight
• gscat – group size category (1, 2 and greater than or equal to 3)
• vis – visibility category (Poor, Good and Excellent)
• glare – whether there was glare (Yes or No)
• ssmi – a measure of ice cover
• altitude – the height of the aircraft in metres
• obsname – unique identifier of observer

The data from the survey has been saved in a .csv file. This file is read into R using read.csv.

crabseal <- read.csv("crabbieMRDS.csv")
str(crabseal)

'data.frame':   3480 obs. of  20 variables:
 $ Study.area  : chr  "Nominal_area" "Nominal_area" "Nominal_area" "Nominal_area" ...
 $ Region.Label: int  1 1 1 1 1 1 1 1 1 1 ...
 $ Area        : int  1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 1000000 ...
 $ Sample.Label: chr  "99A21" "99A21" "99A21" "99A21" ...
 $ Effort      : num  59.7 59.7 59.7 59.7 59.7 ...
 $ distance    : num  144 144 125 125 421 ...
 $ size        : num  1 1 1 1 1 1 1 1 1 1 ...
 $ object      : int  54464 54464 54465 54465 54466 54466 54467 54467 54468 54468 ...
 $ observer    : int  1 2 1 2 1 2 1 2 1 2 ...
 $ detected    : int  1 1 1 1 0 1 1 1 1 1 ...
 $ side        : chr  "R" "R" "L" "L" ...
 $ exp         : num  0 178 212 0 212 ...
 $ fatigue     : num  61.9 61.9 62.6 62.6 62.9 ...
 $ gscat       : int  1 1 1 1 1 1 1 1 1 1 ...
 $ vis         : chr  "G" "G" "G" "G" ...
 $ glare       : chr  "N" "N" "N" "N" ...
 $ ssmi        : int  79 79 79 79 79 79 79 79 79 79 ...
 $ altitude    : num  43.1 43.1 43.1 43.1 43.1 ...
 $ obsname     : chr  "YH" "HZ" "MF" "MH" ...
 $ fold        : int  1 1 2 2 3 3 4 4 5 5 ...

If you’ve used Distance for Windows you might recognize some of the column names from that - indeed the dataset has been exported from Distance for Windows into the .csv file. The first column can be ignored. Region.Label and Area relate to the strata (their names and area - there’s only one in this dataset). Sample.Label and Effort relate to the transects. The columns distance onwards relate to the observations. You can see there are columns for each explanatory variable above, plus one additional one called fold that will enable use to pick a subset of the data (see later on).

Convert the explanatory variables that should be fitted as factor variables into factors.

crabseal$side <- as.factor(crabseal$side)
crabseal$vis <- as.factor(crabseal$vis)
crabseal$glare <- as.factor(crabseal$glare)
crabseal$observer <- as.factor(crabseal$observer)
crabseal$obsname <- as.factor(crabseal$obsname)

Crabeater seal analyses

The observer teams acted independently and so an ‘independent observer’ (IO) configuration can be specified. The code below fits simple models (i.e. distance only) with the full independence assumption and the point independence assumption. For each model, make a note of the estimated values for \(p(0)\) for each observer and the observers combined. Check goodness-of-fit and plot the detection function.

Fit an IO configuration assuming full independence:

# IO configuration - full independence
# MR model - distance only
# Truncation 700m
fi.mr.dist <- ddf(method="io.fi", mrmodel=~glm(link="logit", formula=~distance),
                 data=crabseal, meta.data=list(width=700))
summary(fi.mr.dist)

Summary for io.fi object 
Number of observations   :  1740 
Number seen by primary   :  1394 
Number seen by secondary :  1471 
Number seen by both      :  1125 
AIC                      :  25681.52 


Conditional detection function parameters:
                estimate           se
(Intercept)  2.107762345 0.0994391199
distance    -0.003087713 0.0003159216

                           Estimate           SE          CV
Average p                 0.9071952  0.009684936 0.010675692
Average primary p(0)      0.8916554  0.007472286 0.008380240
Average secondary p(0)    0.8916554  0.007472286 0.008380240
Average combined p(0)     0.9882614  0.004402403 0.004454695
N in covered region    1917.9995344 24.808749358 0.012934700

Next fit IO configuration assuming point independence. Specify a half-normal key function for the DS model; again only include perpendicular distance in the MR model.

# IO configuration - point independence
# MR model - distance only
# DS model - half normal detection function, no additional covars
# Truncation at 700m
pi.mr.dist.ds.hn <- ddf(method="io", dsmodel=~cds(key="hn"),
                 mrmodel=~glm(link="logit", formula=~distance),
                 data=crabseal, meta.data=list(width=700))
summary(pi.mr.dist.ds.hn)

Summary for io.fi object 
Number of observations   :  1740 
Number seen by primary   :  1394 
Number seen by secondary :  1471 
Number seen by both      :  1125 
AIC                      :  3011.463 


Conditional detection function parameters:
                estimate           se
(Intercept)  2.107762345 0.0994391199
distance    -0.003087713 0.0003159216

                        Estimate          SE          CV
Average primary p(0)   0.8916554 0.009606424 0.010773696
Average secondary p(0) 0.8916554 0.009606424 0.010773696
Average combined p(0)  0.9882614 0.002081609 0.002106335


Summary for ds object
Number of observations :  1740 
Distance range         :  0  -  700 
AIC                    :  22314.4 
Optimisation           :  mrds (nlminb) 

Detection function:
 Half-normal key function 

Detection function parameters 
Scale coefficient(s): 
            estimate         se
(Intercept) 5.828703 0.02685781

           Estimate         SE         CV
Average p 0.5845871 0.01247826 0.02134542


Summary for io object
Total AIC value :  25325.86 

                        Estimate          SE         CV
Average p              0.5777249  0.01239167 0.02144909
N in covered region 3011.8139214 79.84149372 0.02650944

Which of these models do you prefer?

If you have time, try a few models with covariates. However, this is a large dataset and so fitting models and obtaining model summaries can take a long time with complicated models. Given this and the fact that the exercise is just for practice, you may want to work with just a subset of the data – which is where the fold column in the dataset comes in. With this column, each observation is associated with a number from 1 to 10 (they are assigned systematically in order of the data, so the first observation is given number 1, the second 2, …, the 10th 10, the 11th 1 again, the 12th 2, etc). So, for example, you could pick out just the first and fifth ``fold’’ (i.e., just one fifth of the data) with

crabseal15 <- crabseal[crabseal$fold %in% c(1, 5), ]

and then use this to investigate covariate selection - for example comparing point independence models where the mr model has just distance in it vs one with distance and observer:

pi.mr.dist.ds.hn.fold15 <- ddf(method="io", dsmodel=~cds(key="hn"),
                 mrmodel=~glm(link="logit", formula=~distance),
                 data=crabseal15, meta.data=list(width=700))
pi.mr.dist.observer.ds.hn.fold15 <- ddf(method="io", dsmodel=~cds(key="hn"),
                 mrmodel=~glm(link="logit", formula=~distance+observer),
                 data=crabseal15, meta.data=list(width=700))
AIC(pi.mr.dist.ds.hn.fold15, pi.mr.dist.observer.ds.hn.fold15)

                                 df      AIC
pi.mr.dist.ds.hn.fold15           3 5068.746
pi.mr.dist.observer.ds.hn.fold15  4 5065.830

Estimating abundance

Following model criticism and selection, the abundance can be estimated – below we use the simple point independence model on the full dataset. The estimates of abundance for the study area are arbitrary because inference of the study was restricted to the covered region, hence, the estimates of abundance here are artificial. Nevertheless, we illustrate the method to estimate abundance. We require tables of the region, transects and detections – these can easily be created from the data using the checkdata function in the Distance package (the ::: is shorthand for accessing a function without loading a package). Using these tables, Horvitz-Thompson-like¹ estimators can be applied to produce estimates of \(\hat{N}\). The use of convert.units=0.001 adjusts the units of perpendicular distance measurement (m) to units of transect effort (km).

# Create tables for estimating abundance 
# Selecting observer==1 ensures that observations in the obs.table are unique 
tables <- Distance:::checkdata(crabseal[crabseal$observer==1, ])

# Estimate abundance in covered region
pi.abund <- dht(model=pi.mr.dist.ds.hn,
                region=tables$region.table, 
                sample=tables$sample.table, obs=tables$obs.table,
                se=TRUE, options=list(convert.units=0.001))

# Pretty tables of data summary
knitr::kable(pi.abund$individuals$summary, digits=3,
      caption="Summary information from crabeater seal aerial survey.")

Summary information from crabeater seal aerial survey.

Region	Area	CoveredArea	Effort	n	k	ER	se.ER	cv.ER	mean.size	se.mean
1	1e+06	8594.082	6138.63	2053	118	0.334	0.033	0.097	1.18	0.013

# Pretty tables of estimates of individual abundance
knitr::kable(pi.abund$individual$N, digits=3,
      caption="Crabeater seal abundance estimates for study area of arbitrary size.")

Crabeater seal abundance estimates for study area of arbitrary size.

Label	Estimate	se	cv	lcl	ucl	df
Total	413493.2	41201.47	0.1	339670.9	503359.5	128.625

Crabeater seals with MCDS (optional)

We can also analyse the crabeater seals data as if it were single platform data (i.e. ignoring that \(p(0)\) is less than 1). These data are available in crabbieMCDS.csv.

This short exercise guides you through the import of these data into R and fits a simple half-normal detection function examining the possible improvement of the model by incorporating side of plane and visibility covariates (using the full dataset).

# Load Distance for MCDS 
library(Distance)
# Read in data
crab.covar <- read.csv("crabbieMCDS.csv")
# Check data imported OK
head(crab.covar, n=3)

    Study.area Region.Label    Area Sample.Label Effort distance size side
1 Nominal_area            1 1000000        99A21  59.72   144.49    1    R
2 Nominal_area            1 1000000        99A21  59.72   125.16    1    L
3 Nominal_area            1 1000000        99A21  59.72   421.40    1    L
    exp fatigue gscat vis glare ssmi altitude obsname fold
1   0.0   61.90     1   G     N   79 43.05763      YH    1
2 211.7   62.61     1   G     N   79 43.05763      MF    2
3   0.0   62.86     1   G     N   79 43.05763      MH    3

After checking that the data have been read into R appropriately, we are ready to fit a detection function.

As before, side of plane and visibility are assigned characters and so we need to tell R to treat them as factors.

# Define factor variables
crab.covar$side <- as.factor(crab.covar$side)
crab.covar$vis <- as.factor(crab.covar$vis)

With two potential explanatory variables, there are a number of possible models. We start by fitting a detection function with side of plane as a covariate using a half-normal key function.

# Fit HN key function with side of plane
ds.side <- ds(crab.covar, key="hn", formula=~side, truncation=700)

Model contains covariate term(s): no adjustment terms will be included.

Fitting half-normal key function

AIC= 22304.742

We would now like to assess the fit of this function to our data. Two visual assessments are provided by the panels below: histogram and fitted function on the left and Q-Q plot on the right.

# Divide plot region
par(mfrow = c(1, 2))
# Create a title for the plot
plot.title <- "Two sets of points\none for each 'side' of plane"
# Plot model
plot(ds.side, pch=19, cex=0.5, main=plot.title)
# Plot qq plot
gof.result <- gof_ds(ds.side, lwd = 2, lty = 1, pch = ".", cex = 0.5)
# Extract gof statistics
message <- paste("CVM GOF p-value=", round(gof.result$dsgof$CvM$p, 4))
# Add gof stats to plot
text(0.6, 0.2, message, cex=0.5)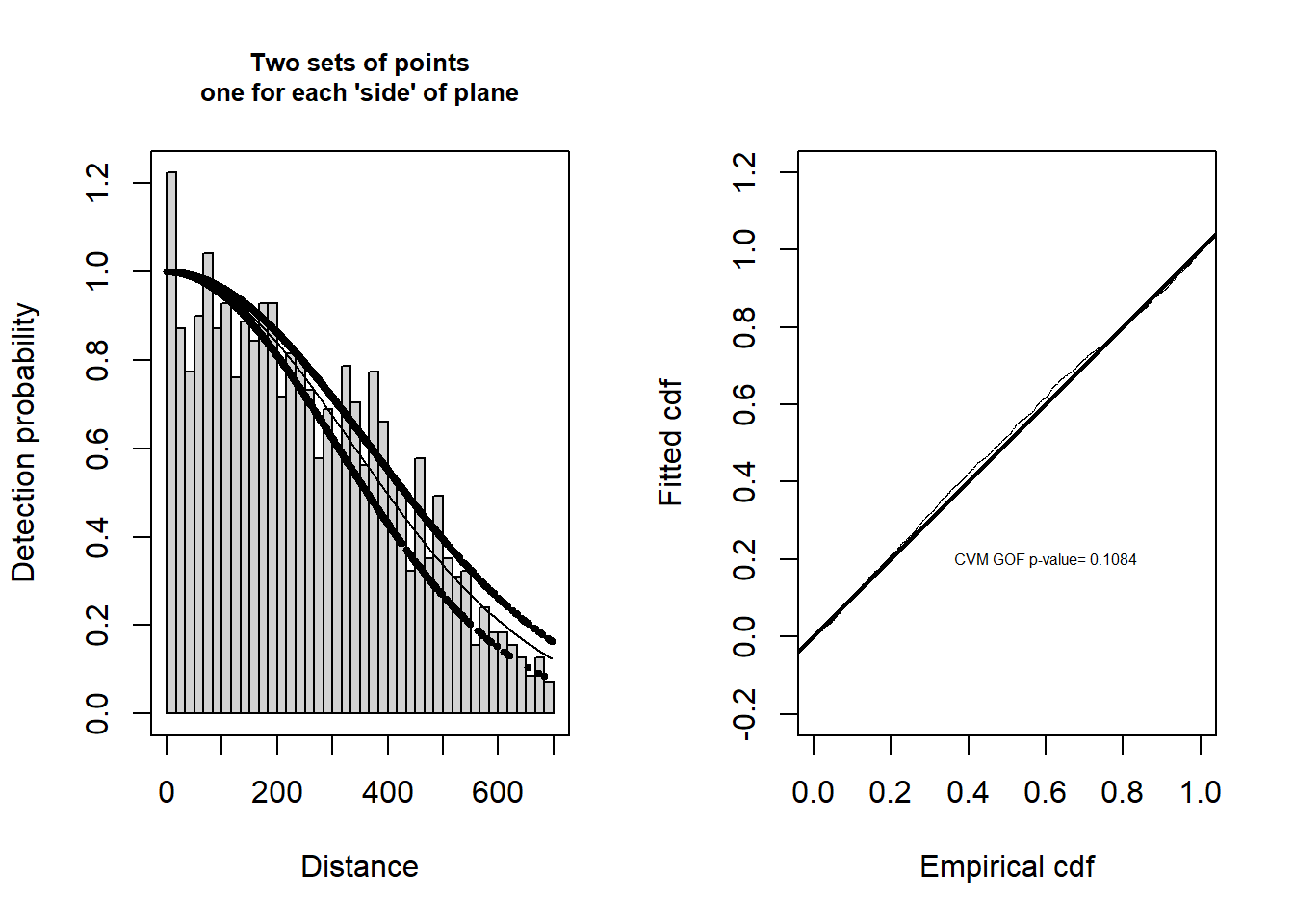

Histogram and fitted half-normal detection function on left. Q-Q plot of detection function and data on right.

The code below fits the model without any covariates.

# Fit HN key function with no covars and no adjustments
ds.nocov <- ds(crab.covar, key="hn", adjustment=NULL, truncation=700)

Fitting half-normal key function

AIC= 22314.398

AIC score for model without covariates is 22314.4 and AIC score for model with side as a covariate is 22304.74 so the model with side as a covariate is preferred.

We could also fit further detection functions and contrast the resulting models:

• with visibility only
• with side of plane and visibility (excluding an interaction).

Out of the four possible models which is to be preferred?

Further modelling is possible. For example, we typically allow adjustment terms in CDS analyses (i.e., where there are not covariates), and it is also possible to include adjustment terms in MCDS analyses. Below is a model with half-normal key and AIC-based selection of cosine adjustments. How does the AIC of this model compare with those fitted previously?

# Fit HN key function with no covars and no adjustments
ds.nocov.hncos <- ds(crab.covar, key="hn", adjustment="cos", truncation=700)

Starting AIC adjustment term selection.

Fitting half-normal key function

AIC= 22314.398

Fitting half-normal key function with cosine(2) adjustments

AIC= 22308.645

Fitting half-normal key function with cosine(2,3) adjustments

AIC= 22304.015

Fitting half-normal key function with cosine(2,3,4) adjustments

AIC= 22305.943

Half-normal key function with cosine(2,3) adjustments selected.

We could go on to produce abundance estimates from our preferred model using the dht function if we had provided information about the size of the crabeater seal study area.

Rather than fitting an MRDS model, as above, would an MCDS analyses have been adequate?

References

Borchers, D. L., Laake, J. L., Southwell, C., & Paxton, C. G. M. (2006). Accommodating unmodeled heterogeneity in double-observer distance sampling surveys. Biometrics, 62, 372–378. https://doi.org/10.1111/j.1541-0420.2005.00493.x

Laake, J., Miller, D., & Petersma, F. (2024). Mrds: Mark-recapture distance sampling. Retrieved from https://github.com/DistanceDevelopment/mrds/

Southwell, C., Borchers, D., de la Mare, B., Paxton, C. G. M., Burt, L., & de la Mare, W. (2007). Estimation of detection probability on aerial surveys of Antarctic pack-ice seals. Journal of Agricultural, Biological, and Environmental Statistics, 12, 1–14. https://doi.org/10.1198/108571107X162920

Thomas, L., Buckland, S. T., Rexstad, E. A., Laake, J. L., Strindberg, S., Hedley, S. L., … Burnham, K. P. (2010). Distance software: Design and analysis of distance sampling surveys for estimating population size. Journal of Applied Ecology, 47(1), 5–14. https://doi.org/https://doi.org/10.1111/j.1365-2664.2009.01737.x

Footnotes

1. \(\hat{N} = \sum_{i=1}^n \frac{1}{\pi_i \hat{p}_i}\) where \(n\) is the number of observations, \(\pi_i\) is the “coverage probability”, i.e., the probability the object is covered by a transect, and \(\hat{p}_i\) is the estimated detection probability, i.e., the probability the object is detected given it is covered by a transect.